Shading is the process of applying a material to an object. It involves determining how light interacts with the surface of the object, including its color, texture, and reflectivity. The shading process is crucial for creating realistic images in computer graphics.
05-CG-Shading
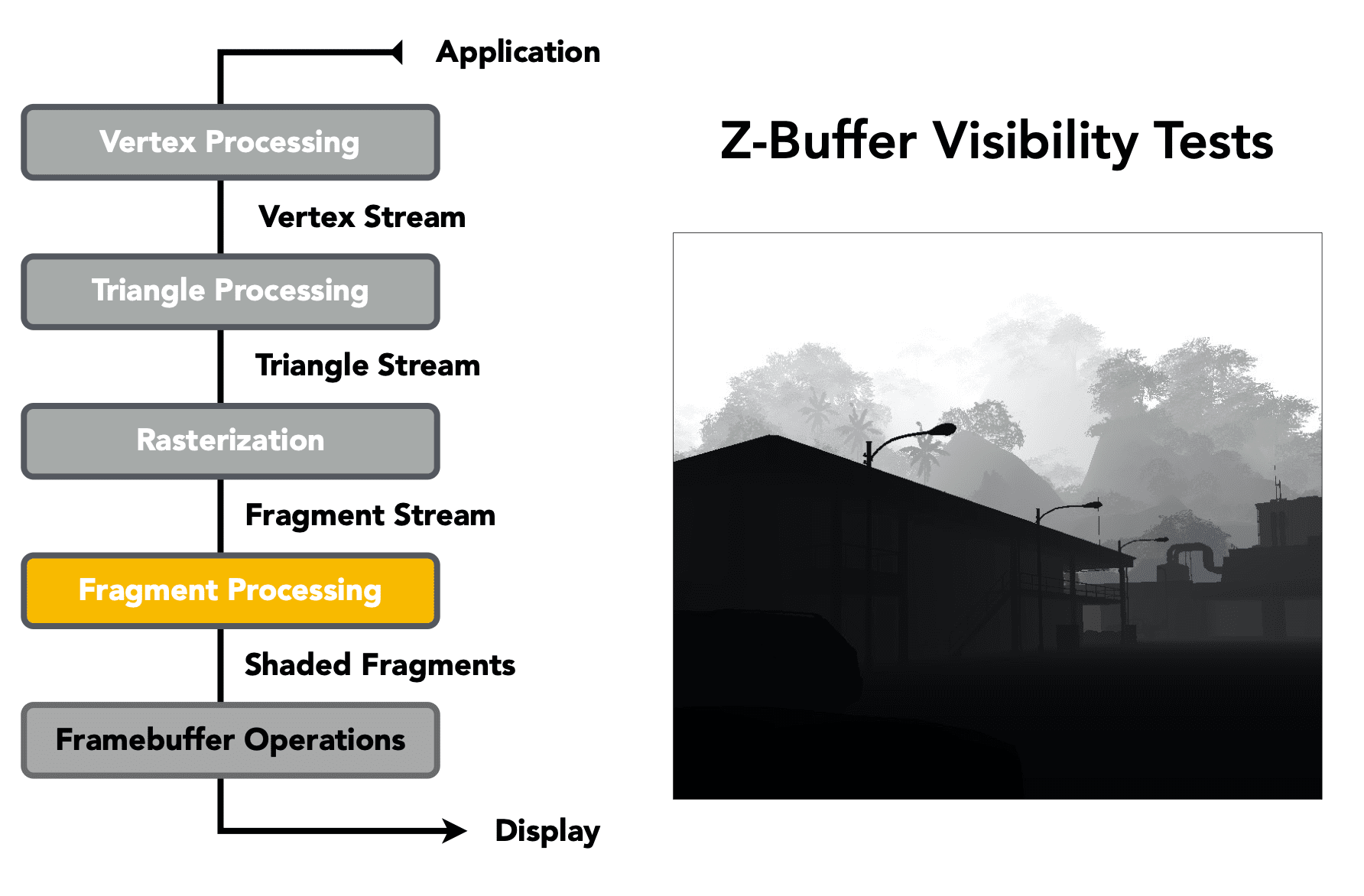
Visibility / Occlusion
- Z-buffering
Shading
- Blinn-Phong reflectance Model
- Shading Models / frequencies
- Graphics Pipeline
- Texture Mapping
- Barycentric Coordinates
- Texture Queries
- Applications of Textures
Visibility / occlusion
Painter's Algorithm
Inspired by how painters paint Paint form back to front, overwrite in the frame buffer
画家算法:由远及近
Requires sorting in depth (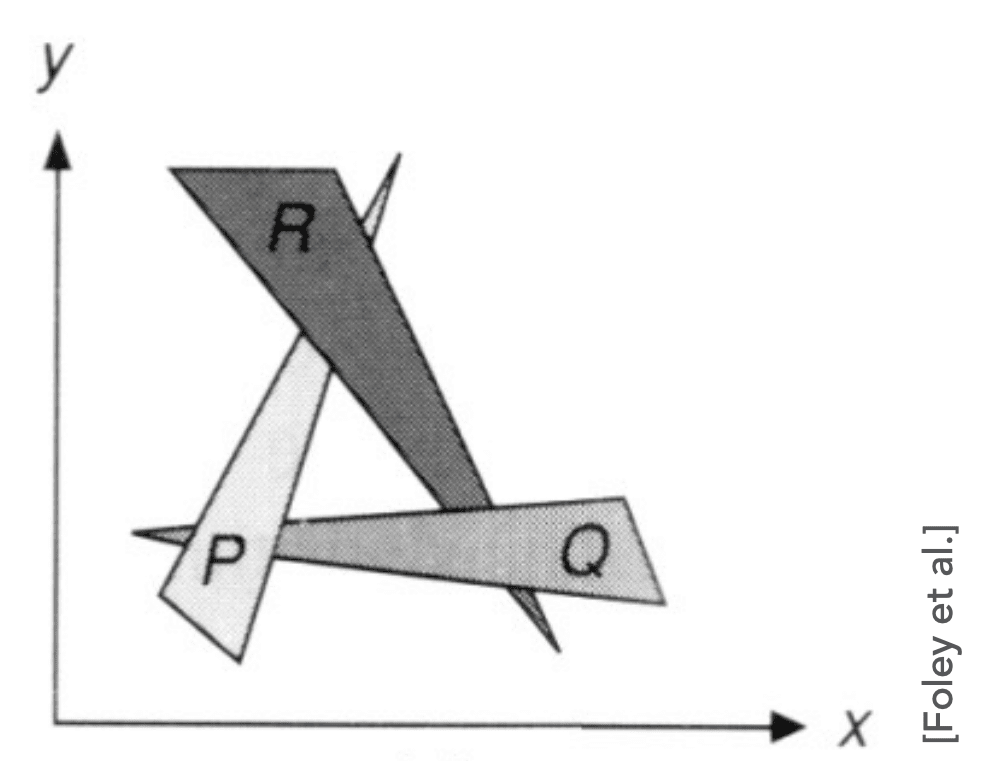
Z-Buffer
This is the algorithm that eventually won.
Idea:
- Store current min. z-value for each sample (pixel)
- Needs an additional buffer for depth values
- frame buffer stores color values
- depth buffer (z-buffer) stores depth
+ IMPORTANT: For simplicity we suppose: *z is always positive*
- smaller z means closer to the camera.
- larger z means farther from the camera.

Z-Buffer Algorithm
Initialize depth buffer to
for (each triangle T)
for (each sample (x,y,z) in T)
if (z < zbuffer[x,y]) // closest sample so far
framebuffer[x,y] = rgb; // update color
zbuffer[x,y] = z; // update depth
else ;// do nothing, this sample is occluded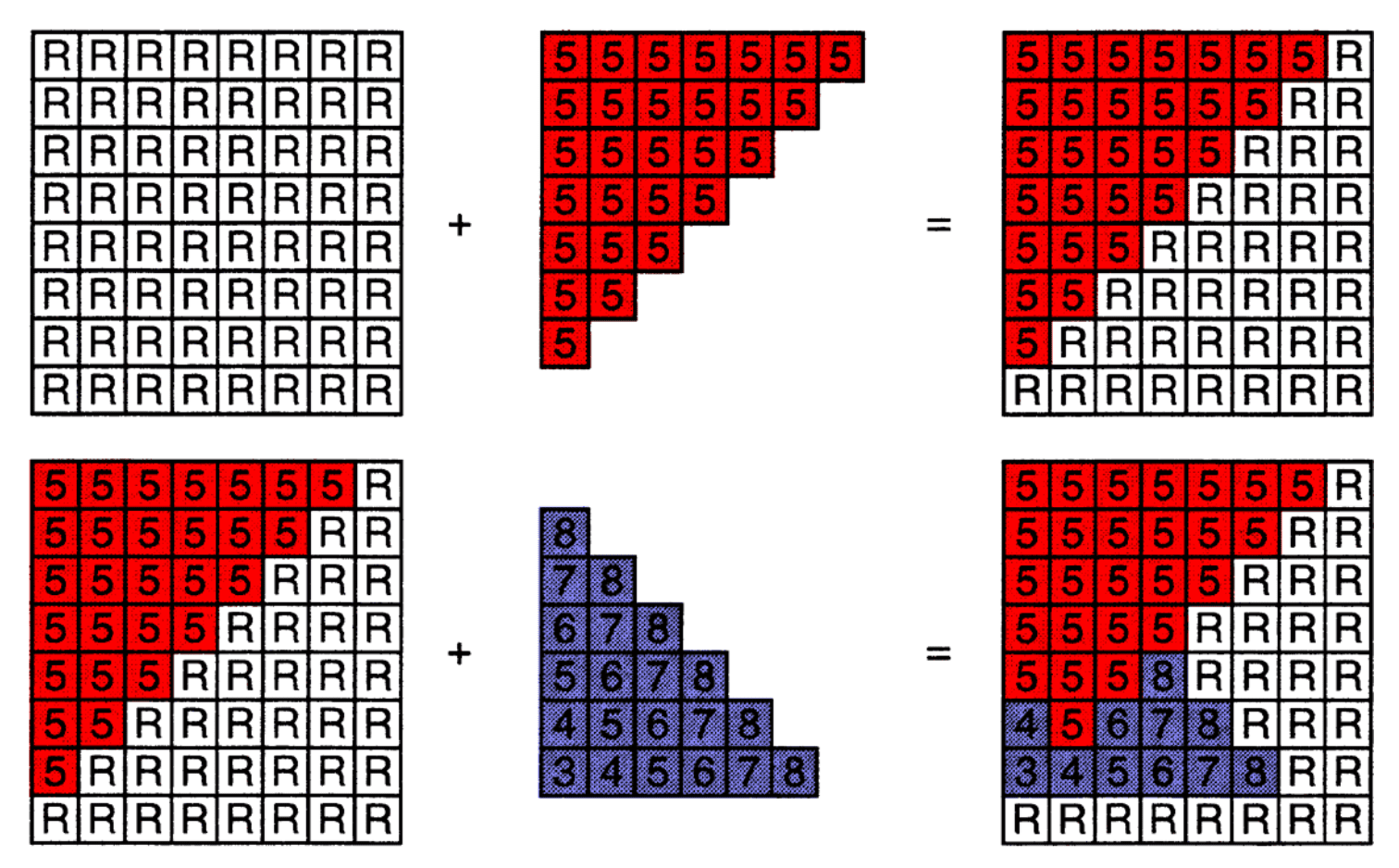
Complexity
for n triangles (assuming constant coverage)
Most important visibility algorithm
- Implemented in hardware for all GPUs
Shading
The darkening or coloring of an illustration or diagram with parallel lines or a block of color.
In Computer Graphics:
- Shading is the process of applying a material to an object.
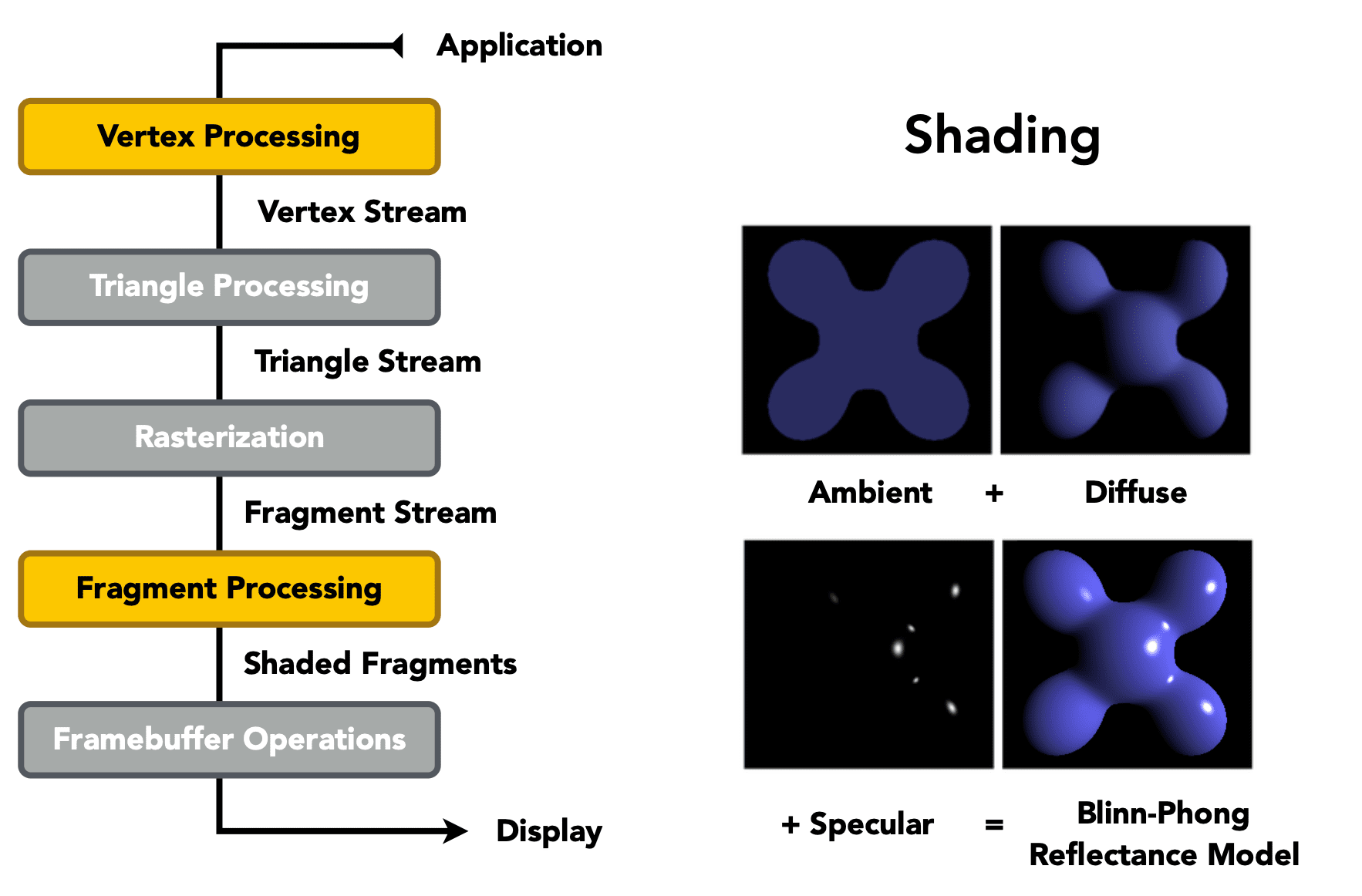
A Simple Shading Model: (Blinn-Phong Reflection Model)
Perceptual Observations
- Specular Highlights 镜面高光
- Diffuse Reflection 漫反射
- Ambient Lighting 环境光

Shading is Local
阴影是局部的
Compute light reflected toward camera at a specific shading point
Inputs: All of the following is unit vectors
- Viewer direction,
- Surface normal,
- Light direction,
(for each of many lights) - Surface parameters (color, shininess, ...)
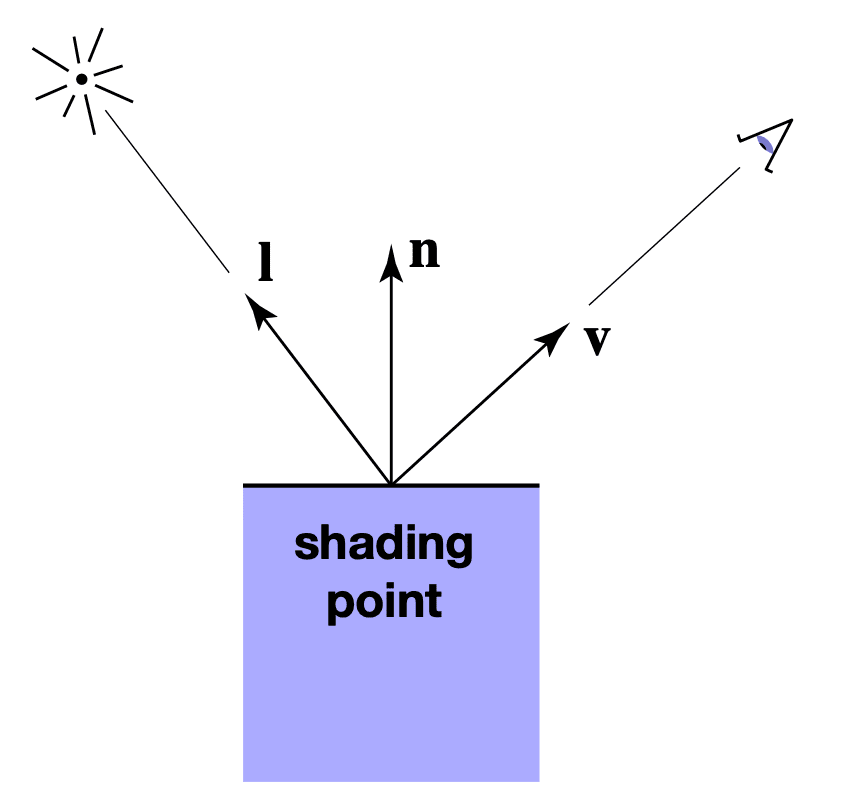
No Shadows will be generated! (Shading
Diffuse Reflection
Light is scattered uniformly in all directions
- Surface color is the same for all viewing directions
How much light (energy) is received?
- Lambert’s cosine law
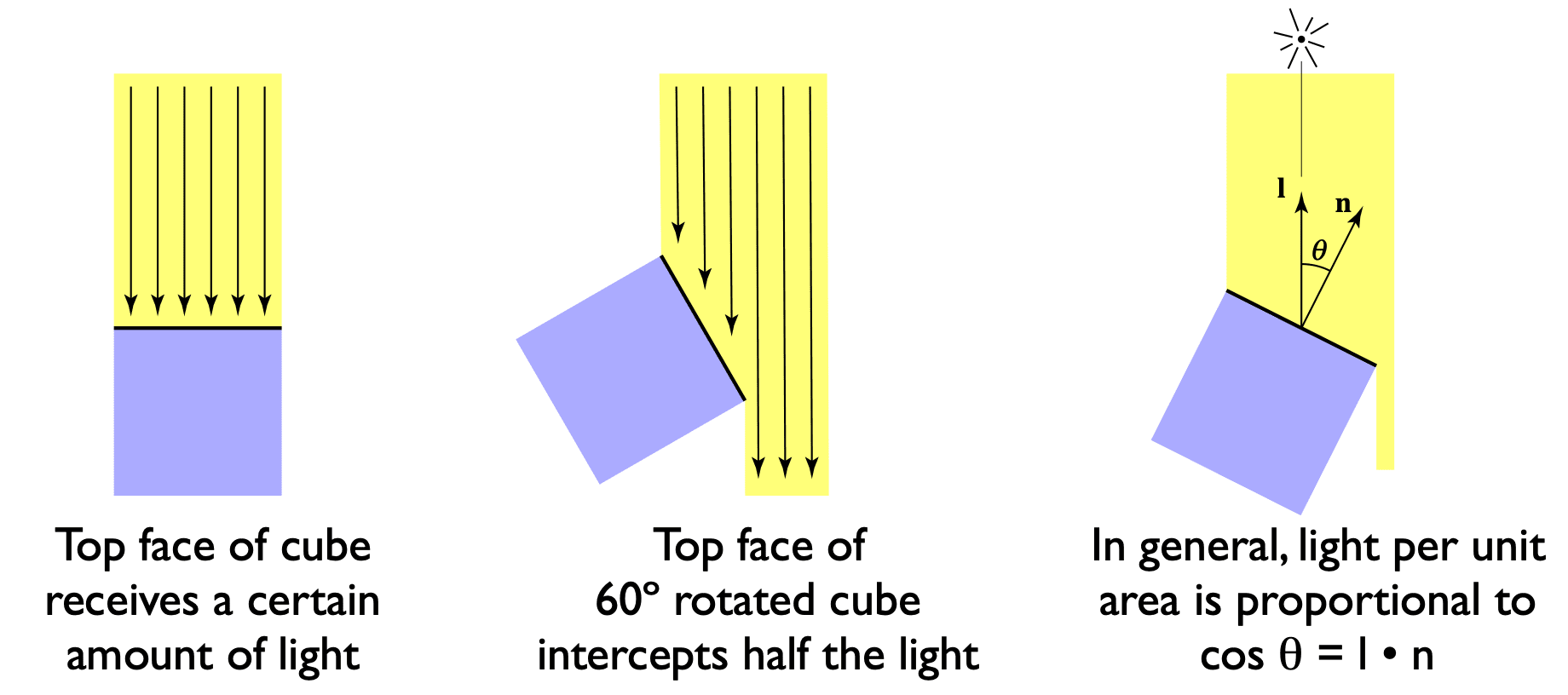
- Lighting Falloff
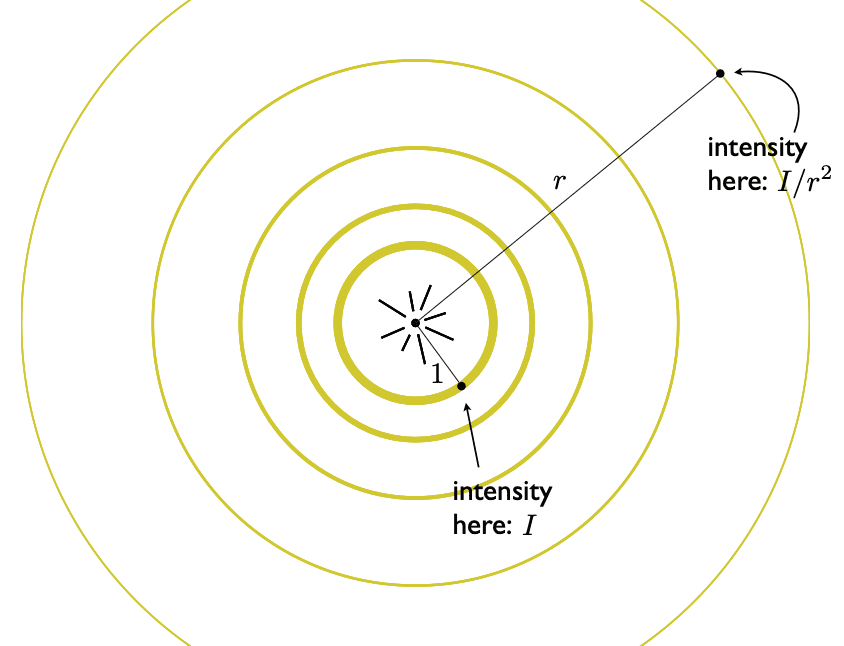
Shading independent of view direction 在任意方向观察,颜色都一样
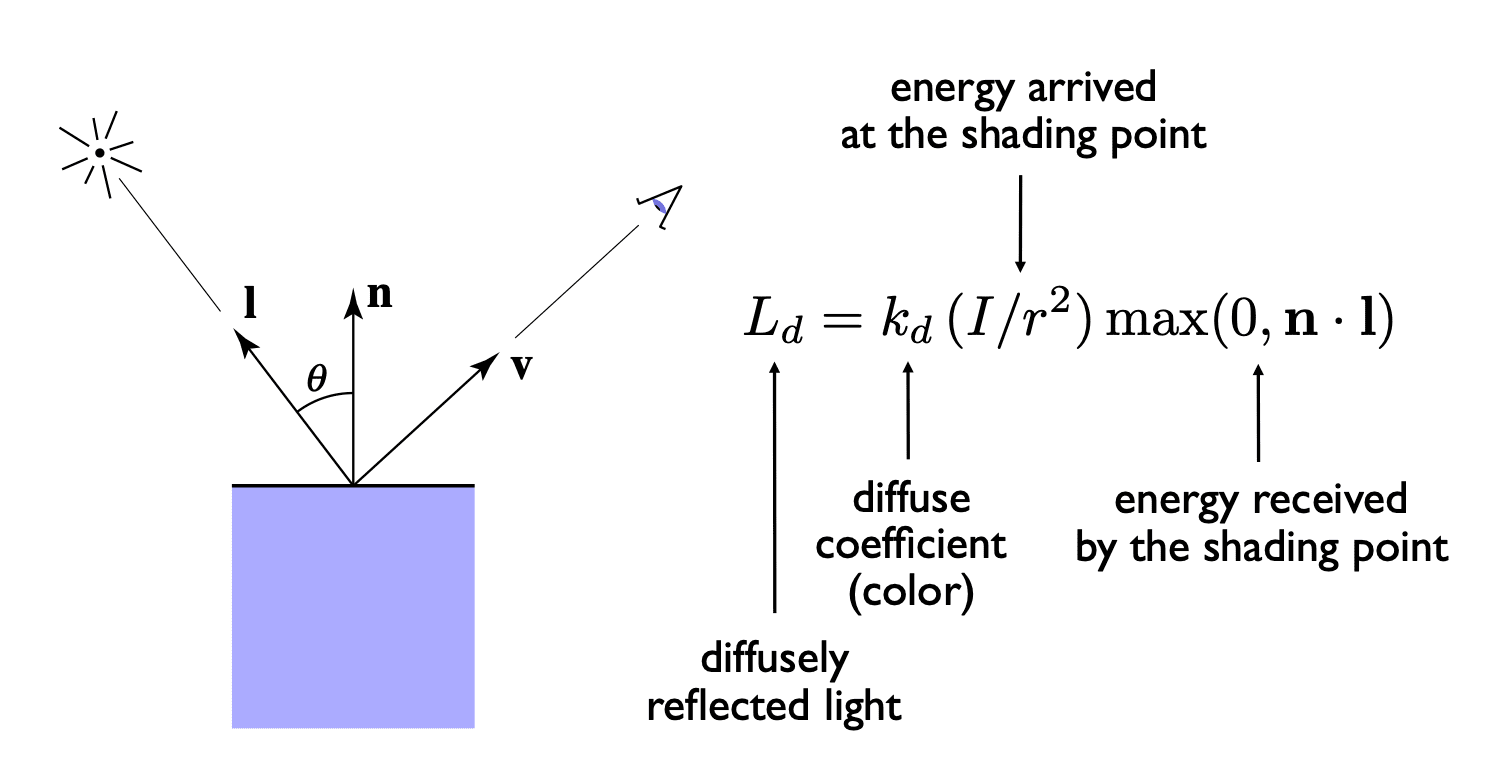
Energy arrived at the shading point
: diffuse coefficient (color) : energy received by the shading point : diffusely reflected light : cosine of angle between light direction and surface normal

Specular Reflection
Intensity depends on view direction
- Bright near mirror reflection direction
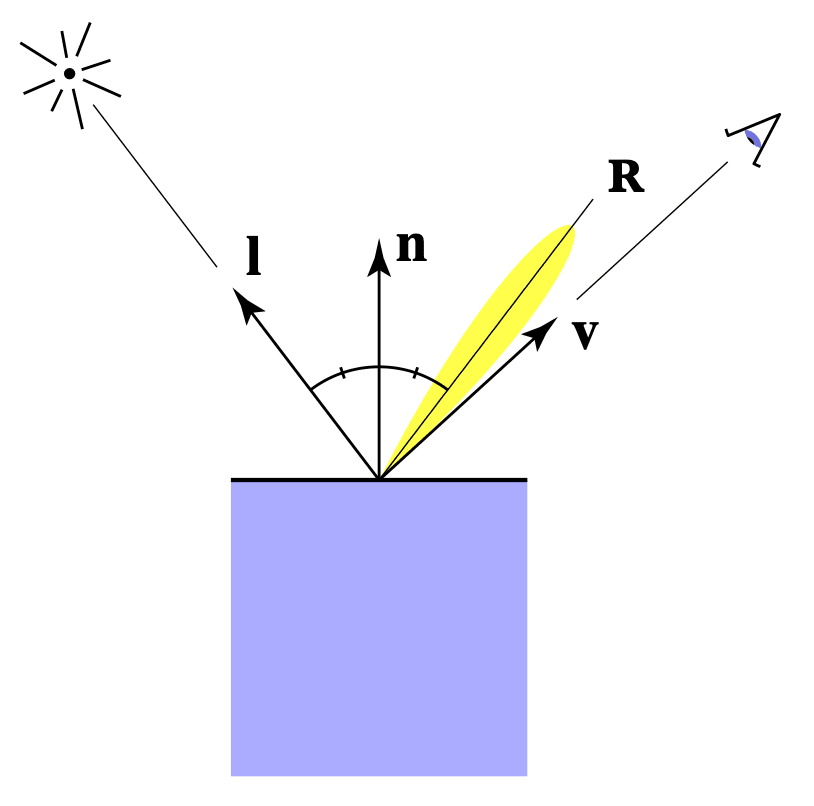
V close to mirror direction
- Measure "near" by dot product of unit vectors
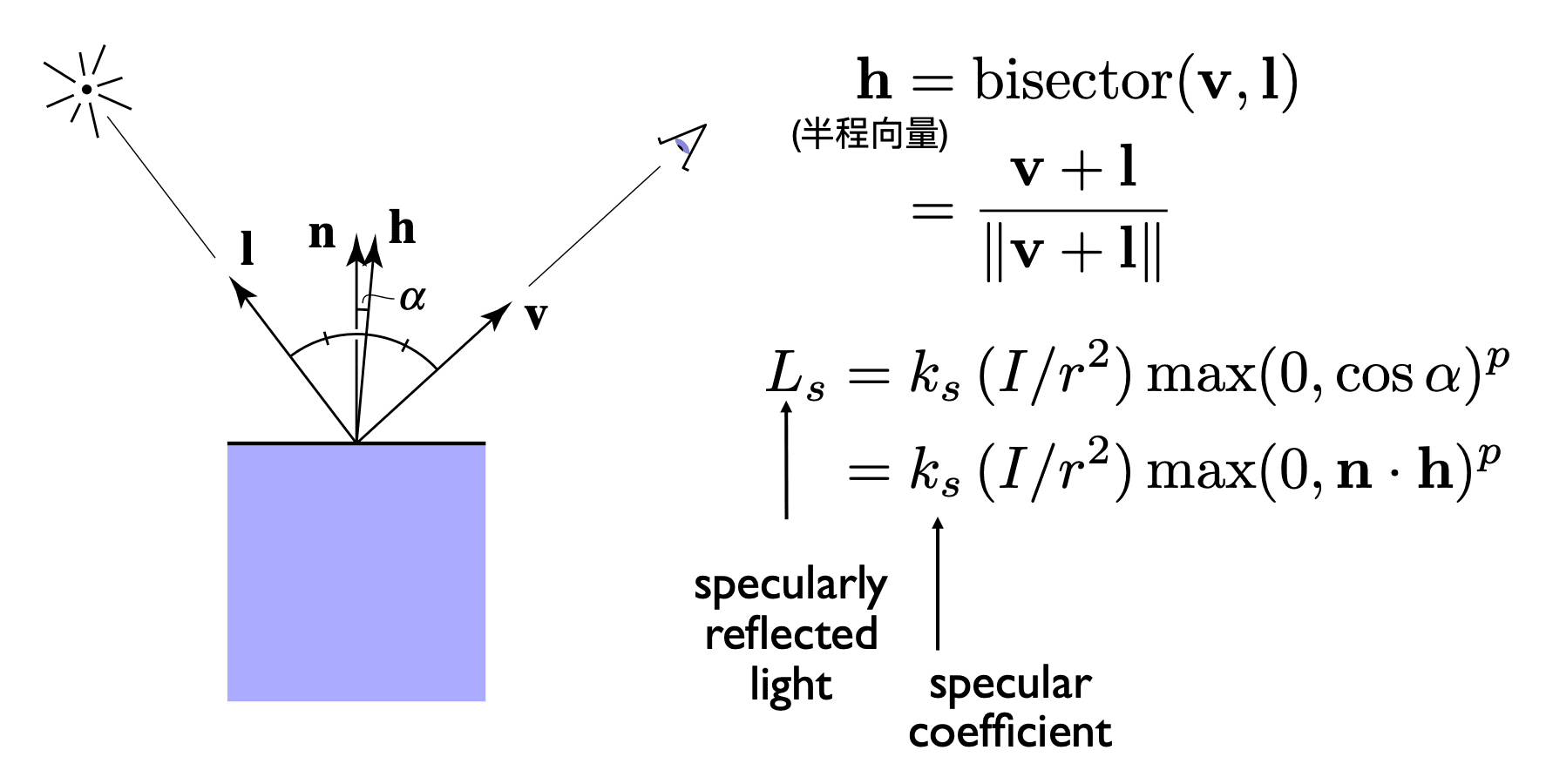
(半程向量)
: specular coefficient : specularly reflected light : specular exponent (shininess)
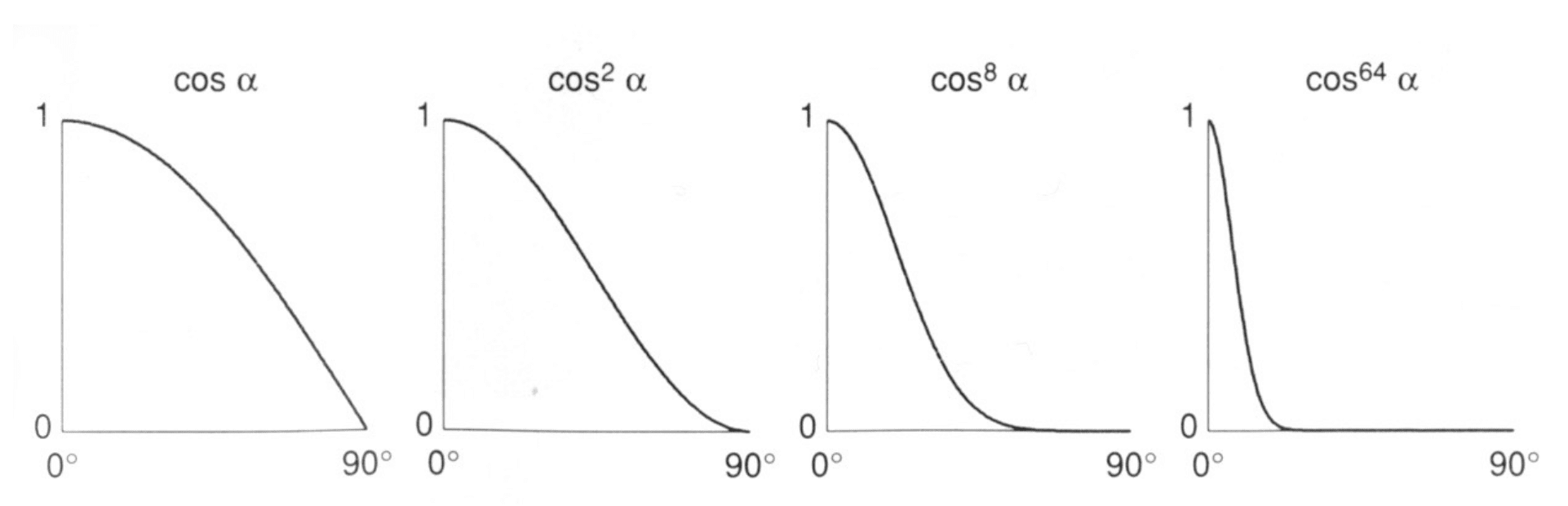
- Increasing
narrows the reflection lobe.

Ambient Lighting
Shading that does not depend on anything
- Add constant color to account for disregarded illumination and fill in black shadows
- This is approximate / fake!
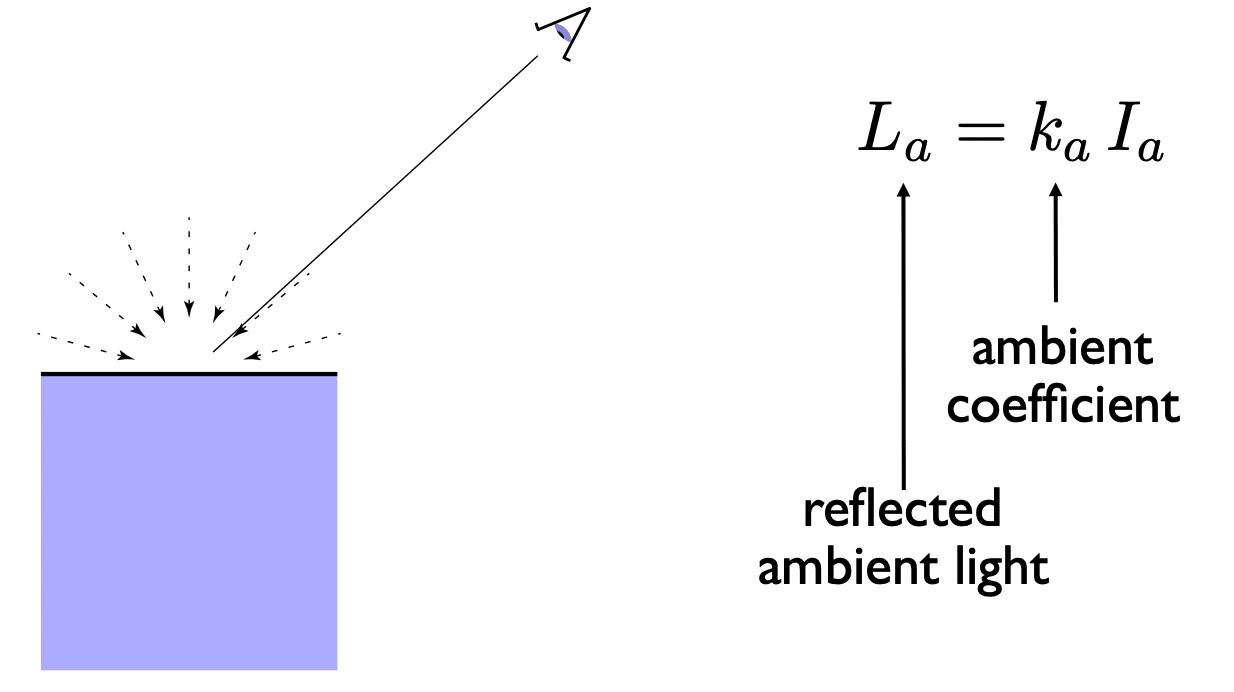
保证没有地方是黑的
: ambient coefficient : reflected ambient light
Blinn-Phong Reflection Model

Shading Frequencies

- Flat shading: Shade each triangle
- Gouraud shading: Shade each vertex
- Phong Shading: Shade each pixel
Flat Shading
- Triangle face is flat — one normal vector
- Not good for smooth surfaces

Gouraud shading
- Interpolate colors from vertices across triangle
- Each vertex has a normal vector

Phong Shading
- Interpolate normal vectors across each triangle
- Compute full shading model at each pixel
- Not the Blinn-Phong Reflectance Model


当渲染图形较为简单时,可以采用着色频率较低的着色方法,来提高渲染速度。
Defining Per-Vertex Normal Vectors
Best to get vertex normals from the underlying geometry
- e.g. consider a sphere
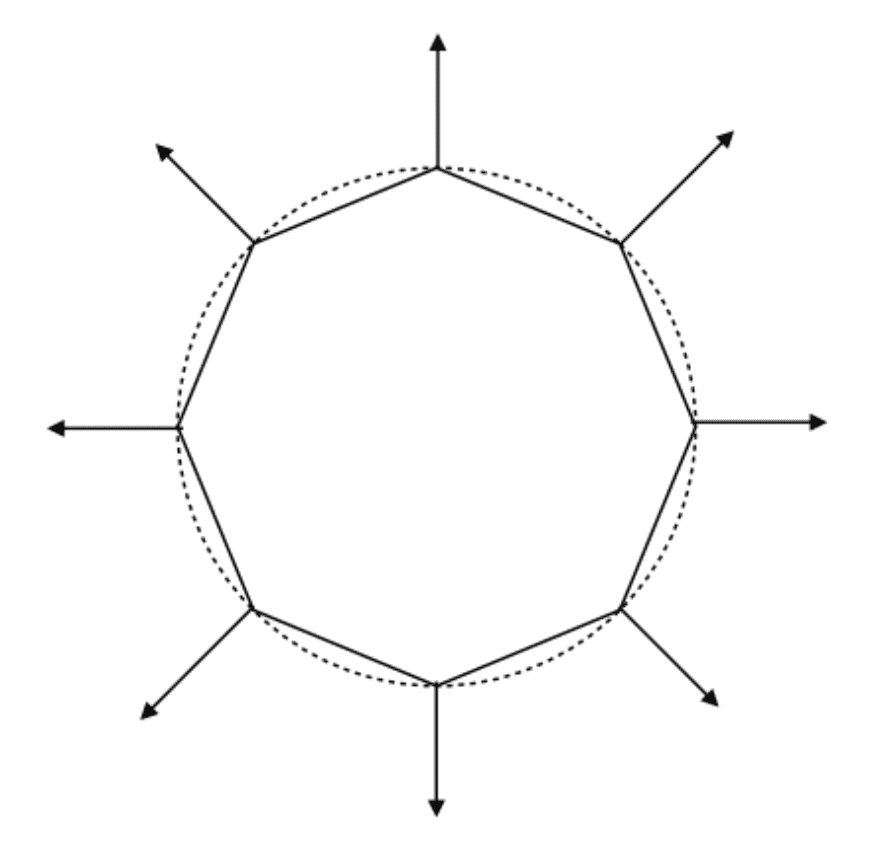
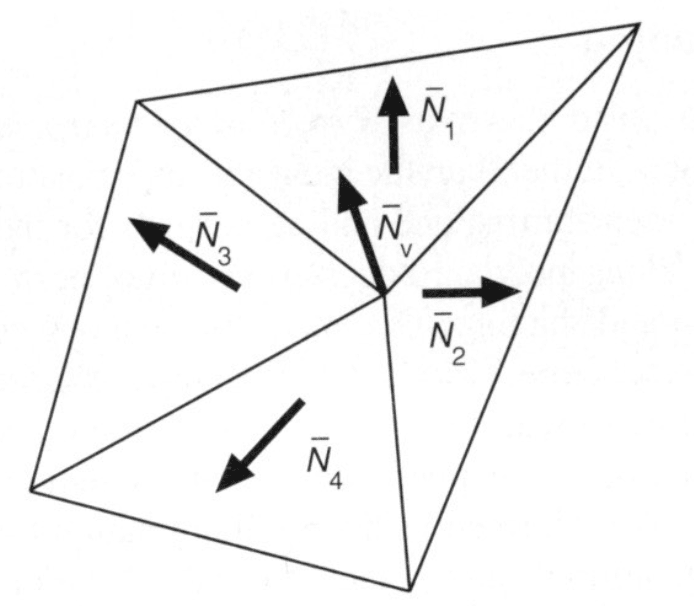
Otherwise have to infer vertex normals from triangle faces
- Simple scheme: average surrounding face normals
Defining Per-Pixel Normal Vectors
Barycentric interpolation of vertex normals
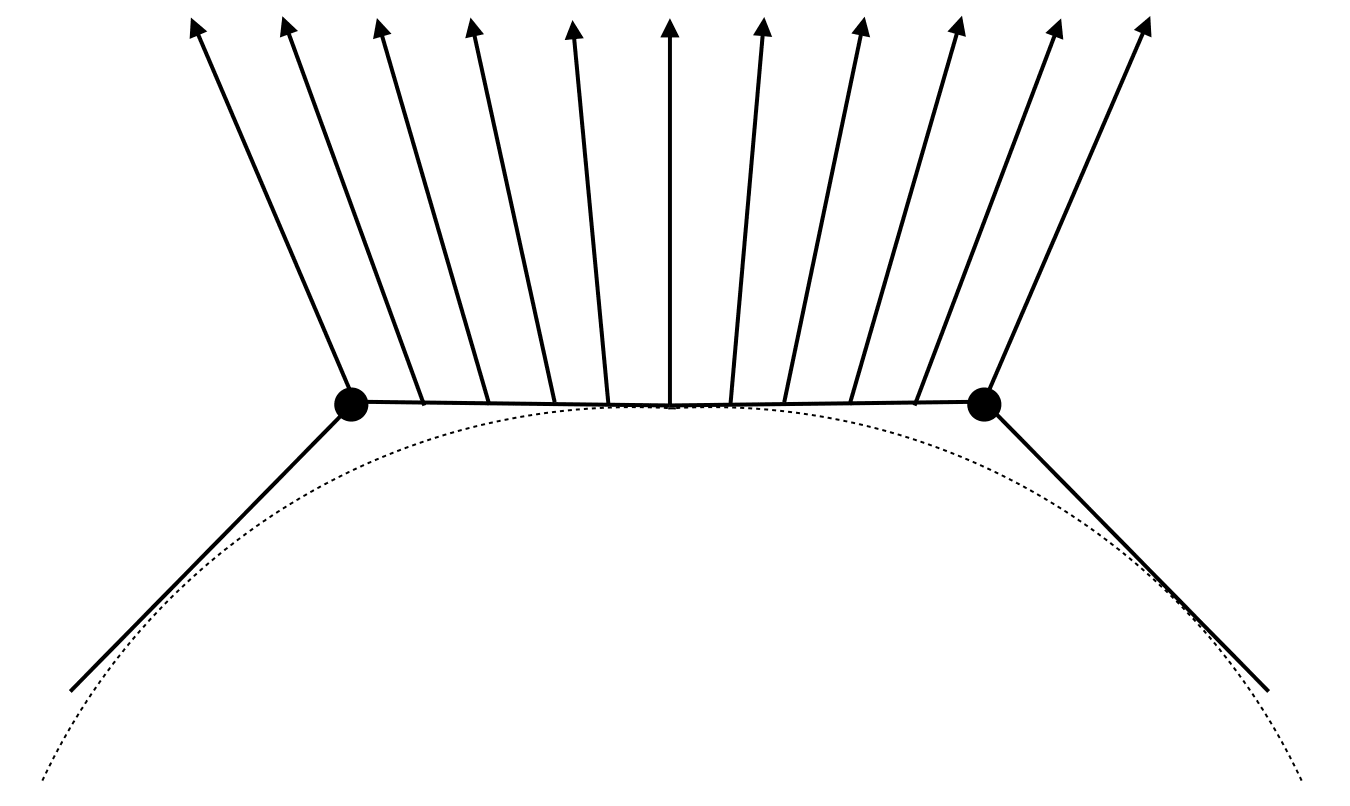
Don’t forget to normalize the interpolated directions.
Graphics Pipeline
(Real-time Rendering)
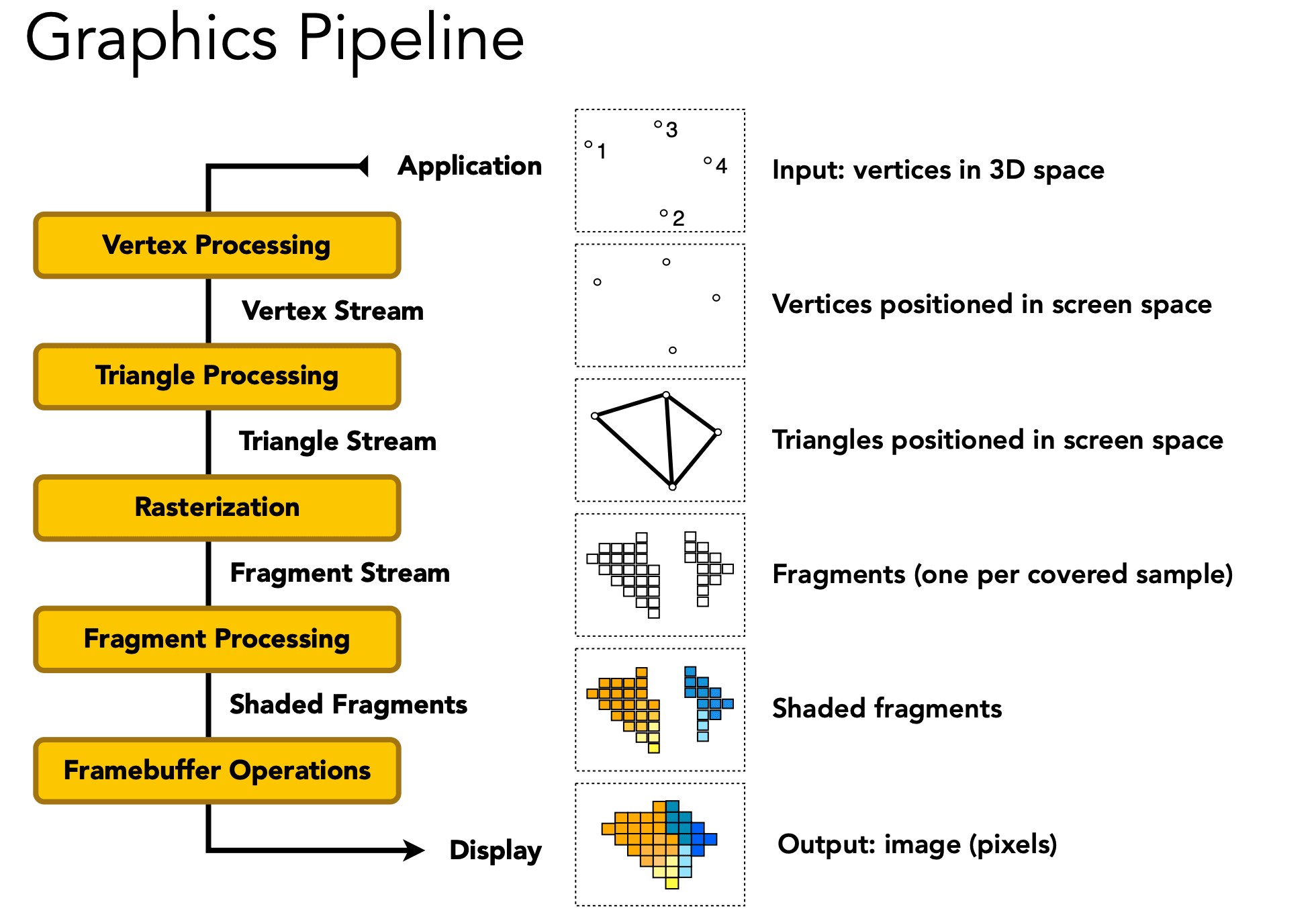
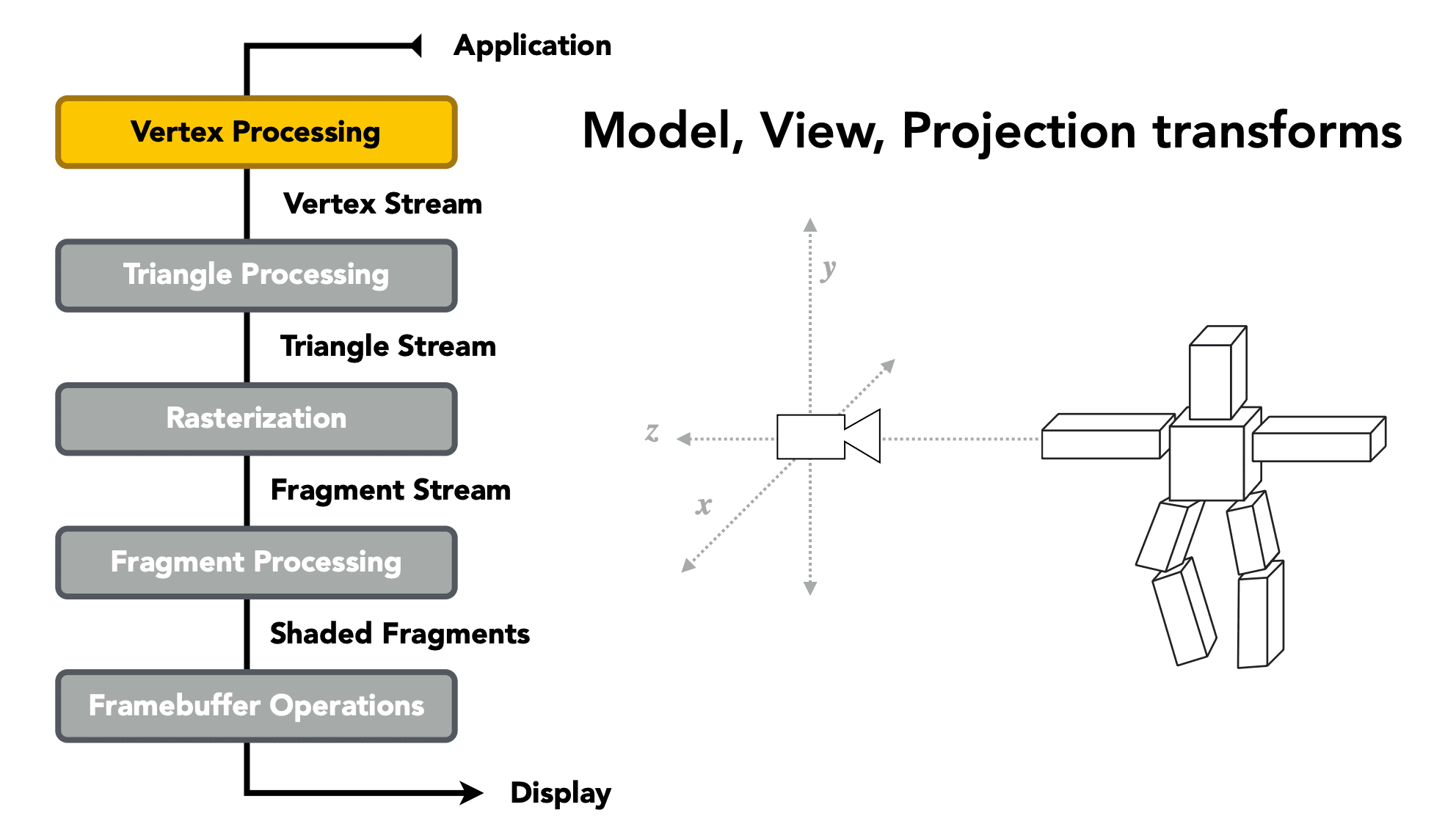
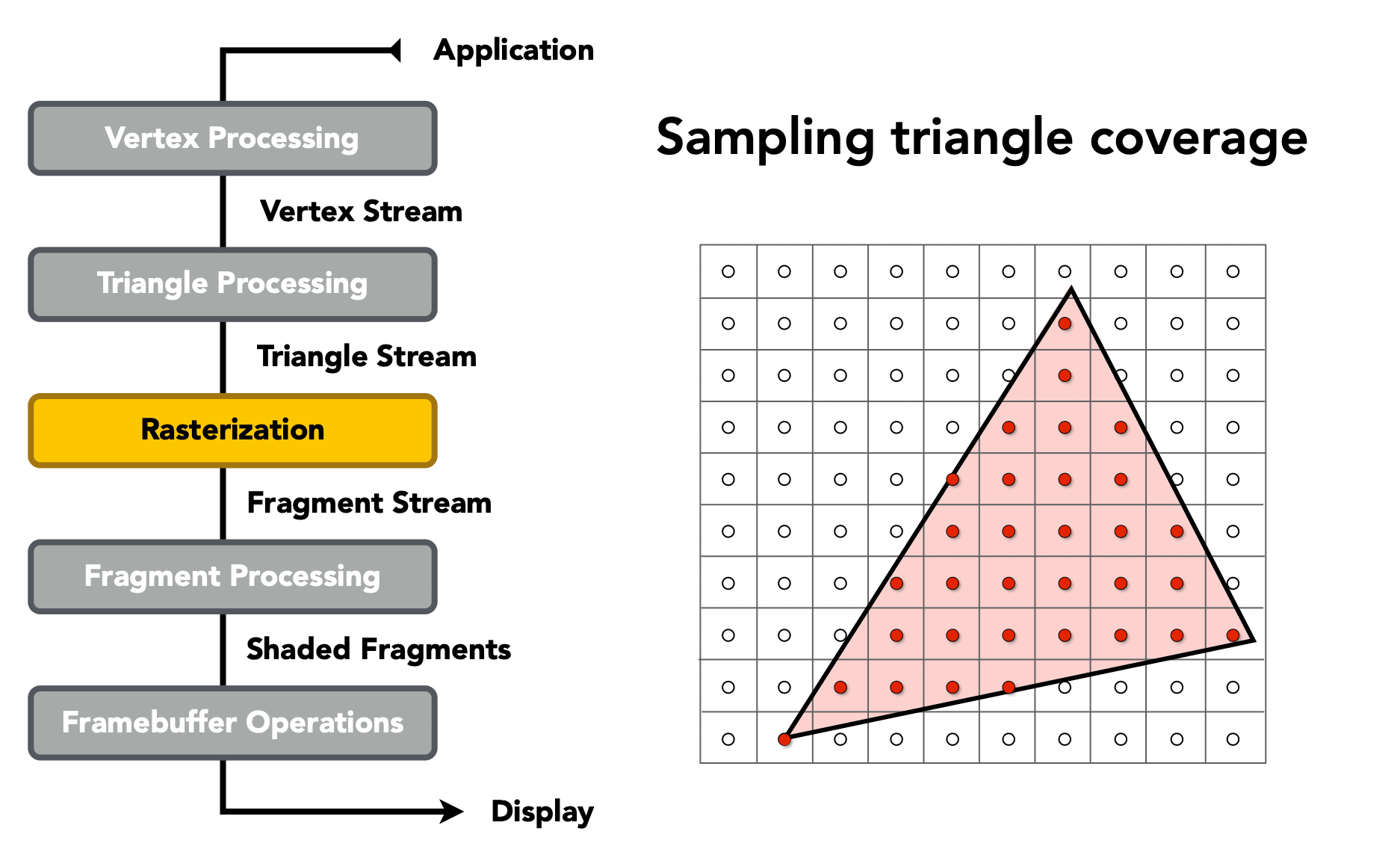
Shader Programs
- Program vertex and fragment processing stages
- Describe operation on a single vertex (or fragment)
Example GLSL fragment shader program
uniform sampler2D myTexture; // program parameter
uniform vec3 lightDir;// program parameter
varying vec2 uv; // per fragment value (interp. by rasterizer)
varying vec3 norm; // per fragment value (interp. by rasterizer)
void diffuseShader(){
vec3 kd;
kd = texture2d(myTexture, uv); // material color from texture
kd *= clamp(dot(-lightDir, norm), 0.0, 1.0); // Lambertian shading model
gl_FragColor = vec4(kd, 1.0); // output fragment color
}- Shader function executes once per fragment.
- Outputs color of surface at the current fragment's screen sample position.
- This shader performs a texture lookup to obtain the surface's material color at this point, then performs a diffuse lighting calculation.
Texture Mapping
Surfaces are 2D
- Surface lives in 3D world space
- Every 3D surface point also has a place where it goes in the 2D image (texture).
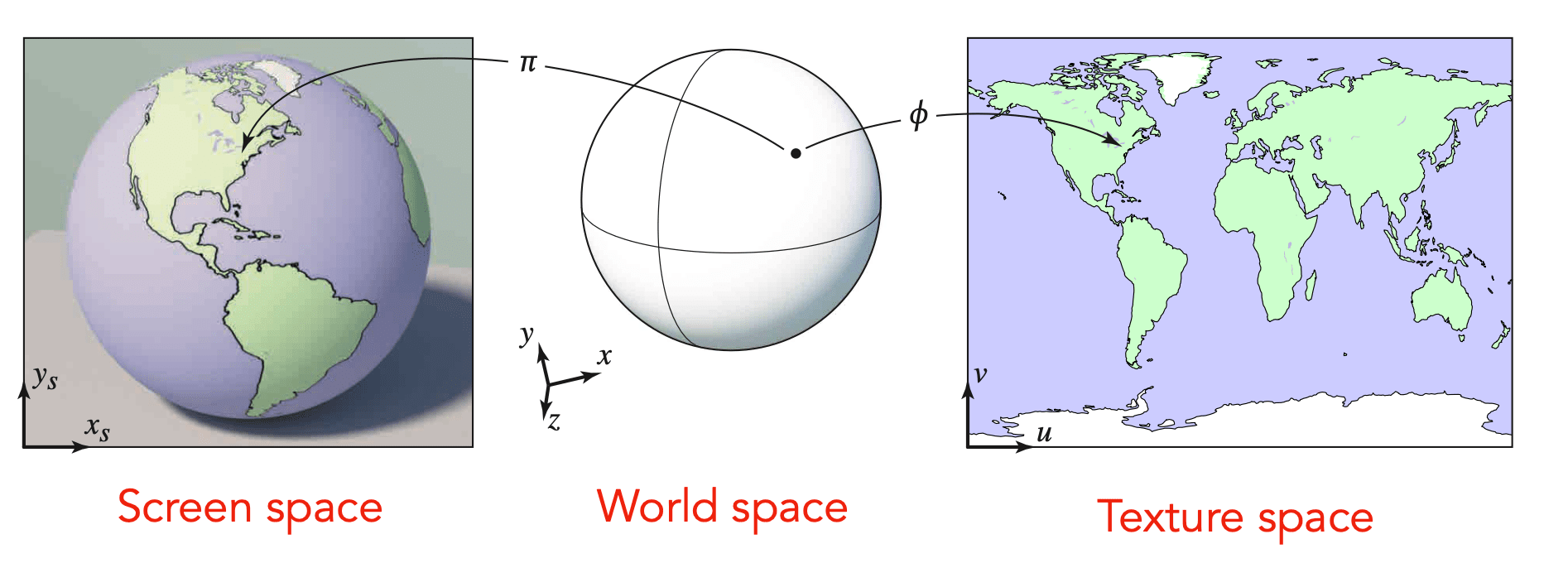

Visualization of Texture Coordinates
Each triangle vertex is assigned a texture coordinate
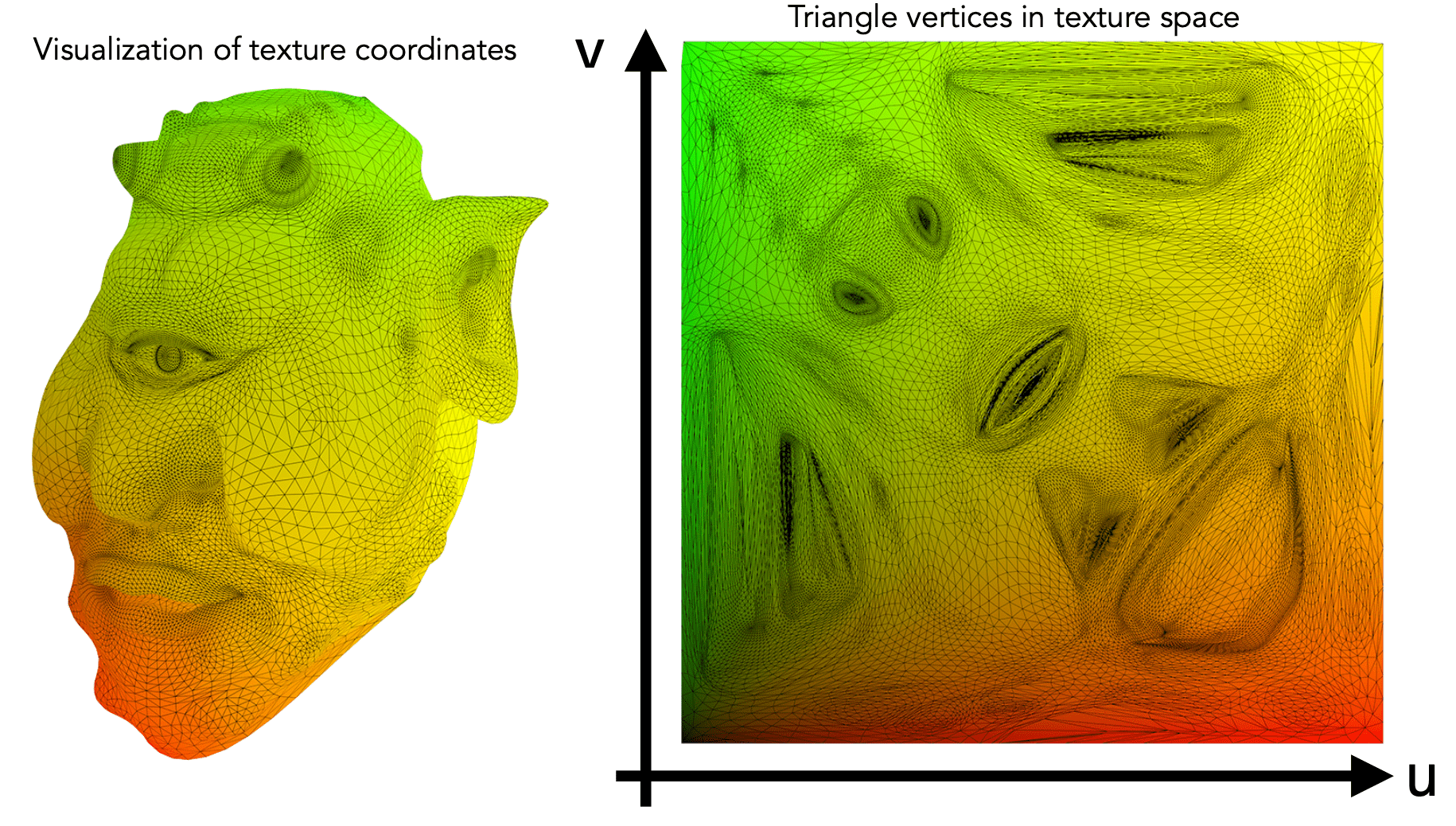
Textures can be used multiple times!

Interpolation Across Triangles
Why do we want to interpolate?
- Specify values at vertices
- Obtain smoothly varying values across triangles.
What do we want to interpolate?
- Texture coordinates, colors, normal vectors,
How do we interpolate?
- Barycentric Coordinates 重心坐标
Barycentric Coordinates
A coordinate system for triangles
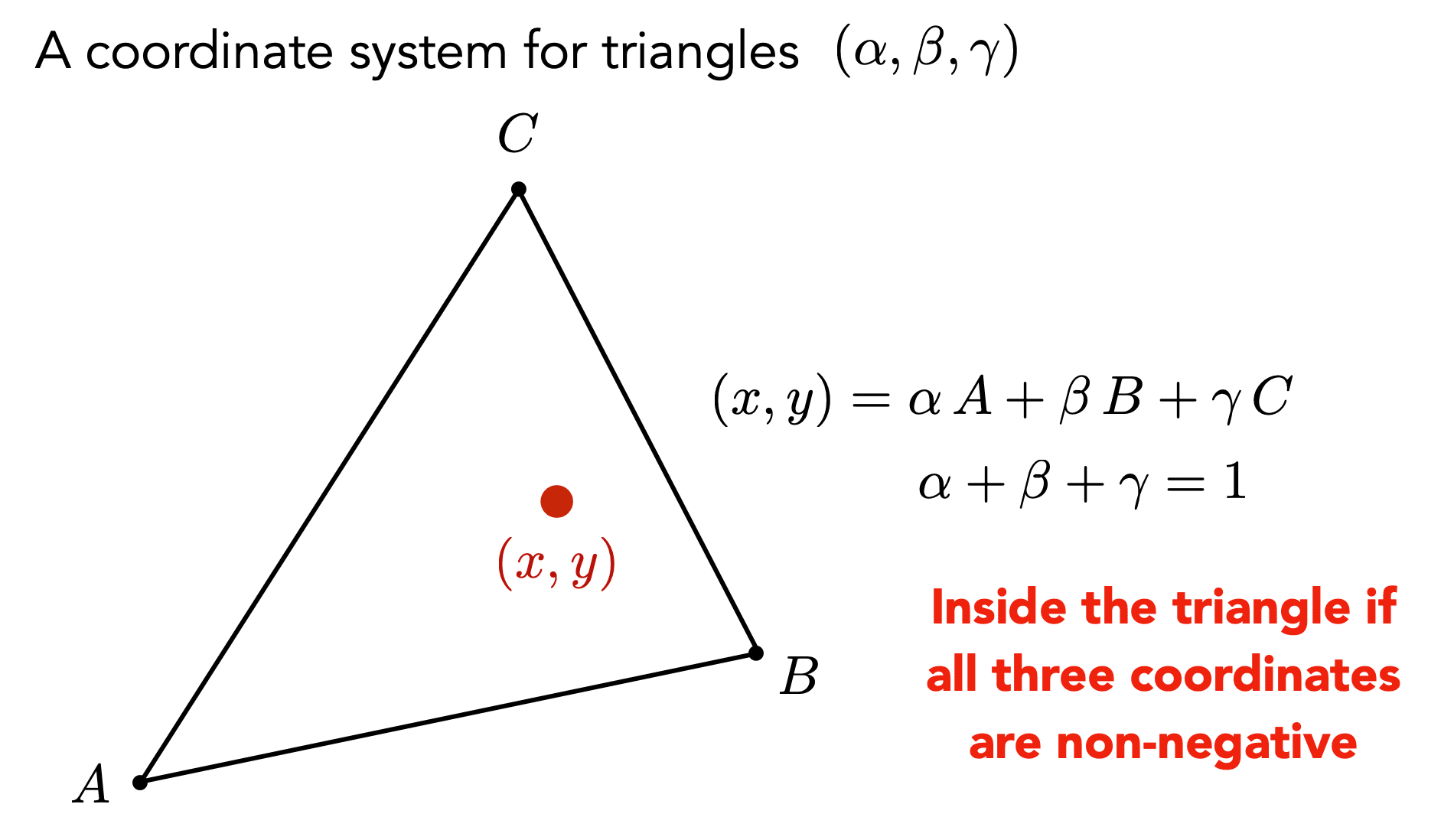
Eample: Point A:
Geometric viewpoint - proportional areas
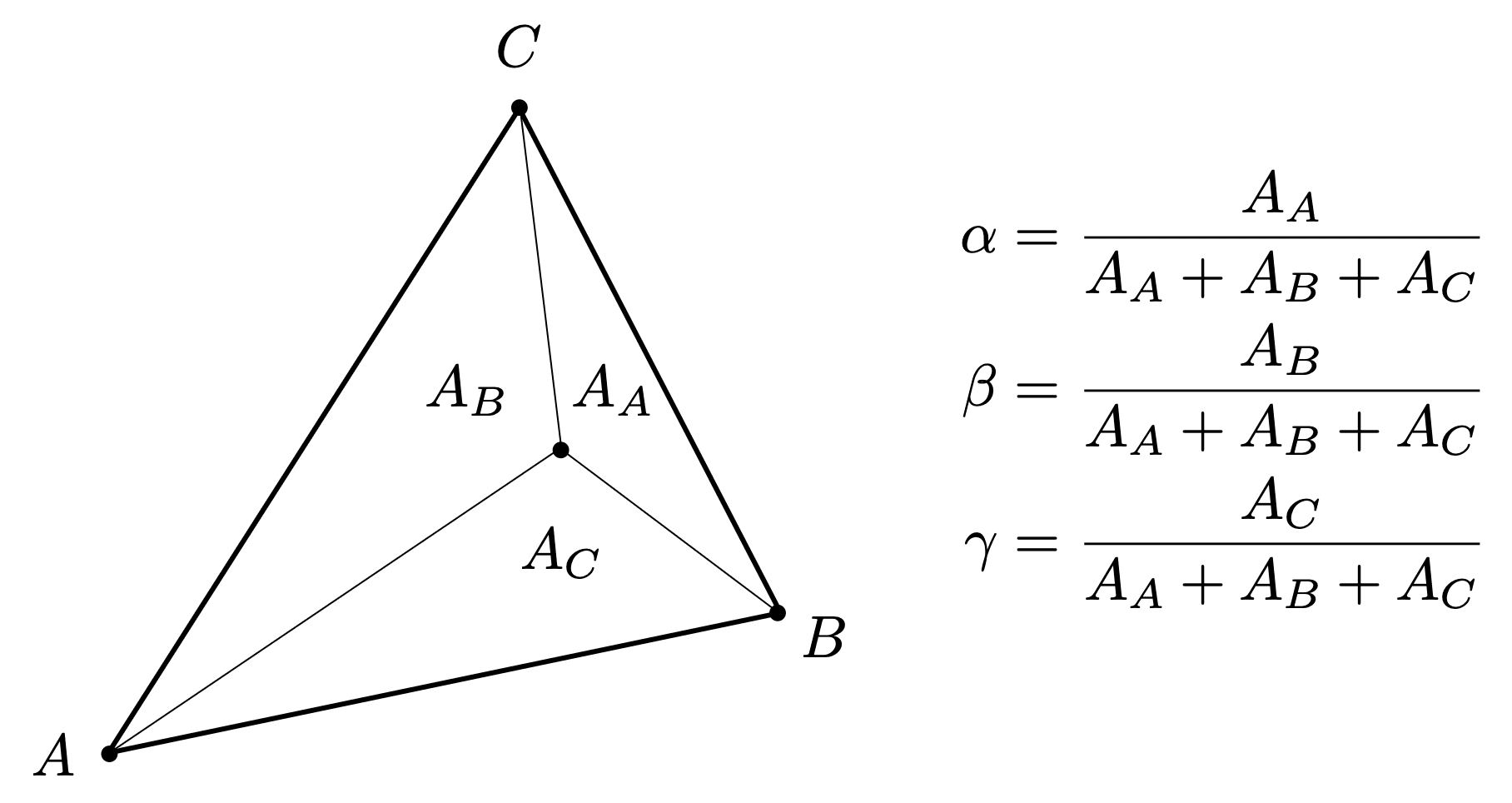
What is the barycentric coordinates of the centroid? 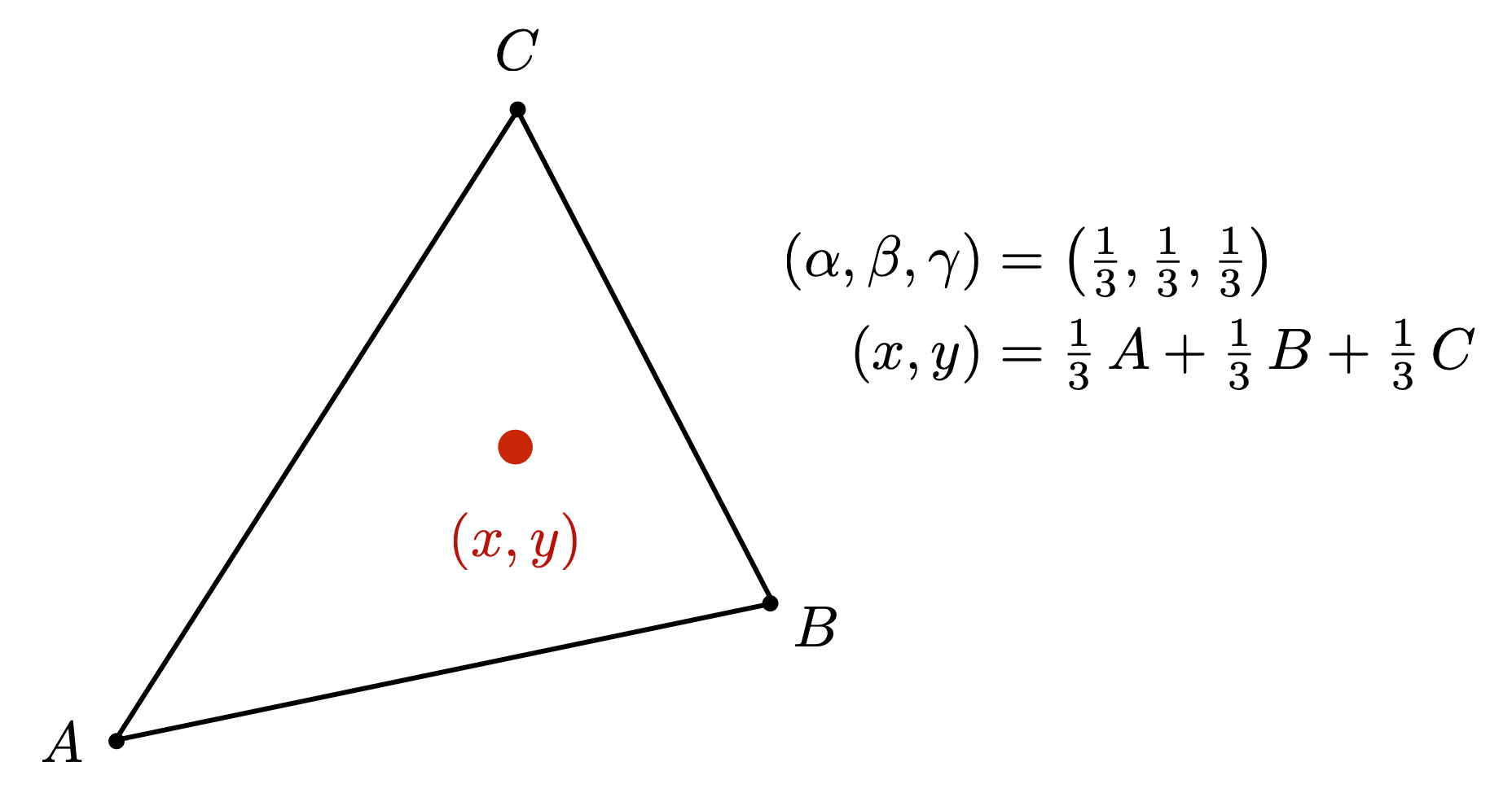
Barycentric Coordinates: Formulas
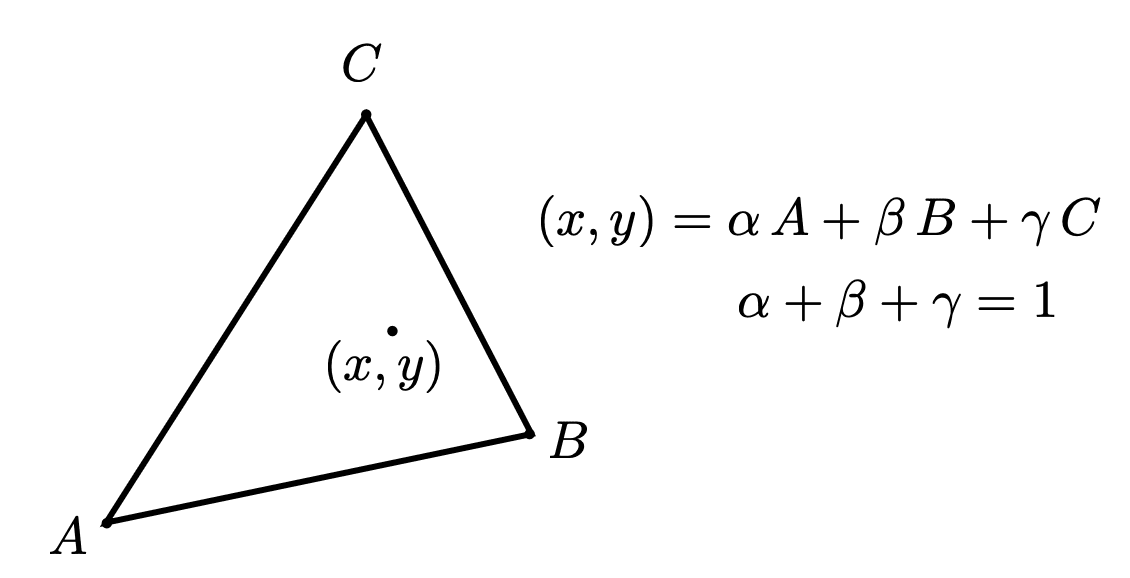
Using Barycentric Coordinates
Linearly interpolate values at vertices
V could be positions, texture coordinates, color, normal, depth, material attributes,
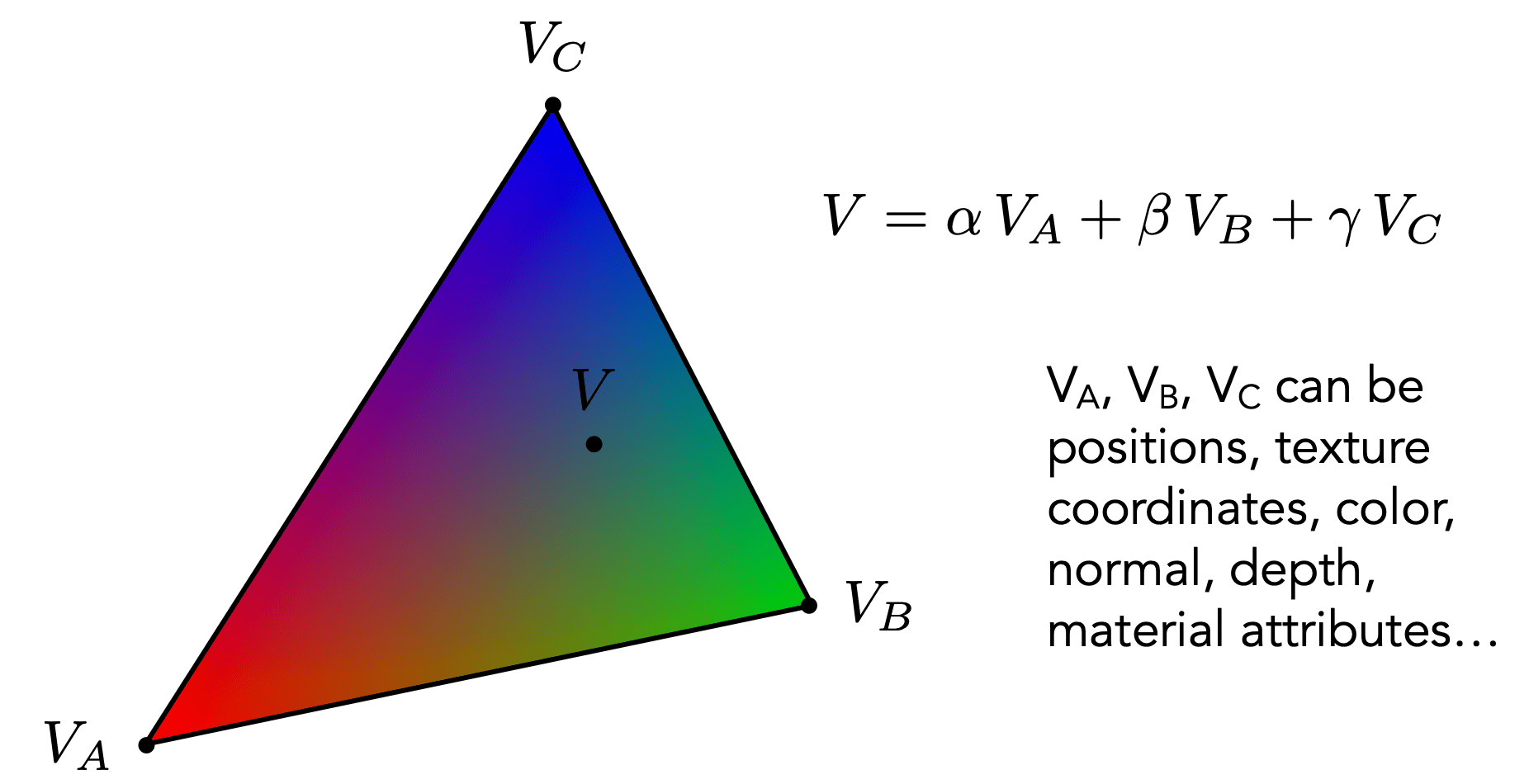
However, barycentric coordinates are not invariant under projection!
Applying Textures
Simple Texture Mapping: Diffuse Color
for each rasterized screen sample (x,y):
(u,v) = evaluate texture coordinate at (x,y)
texcolor = texture.sample(u,v);
set sample's color to texcolor;: Usually a pixel's center : using barycenteric coordinates - set sample's color to texcolor: Usually the diffuse albedo Kd (Bling-Phong reflectance model)
Texture Magnification
What if the texture is too small?
Generally don't want this - Insufficient texture resolution A pixel on a texture - a texel (纹理元素,纹素)
Bilinear interpolation
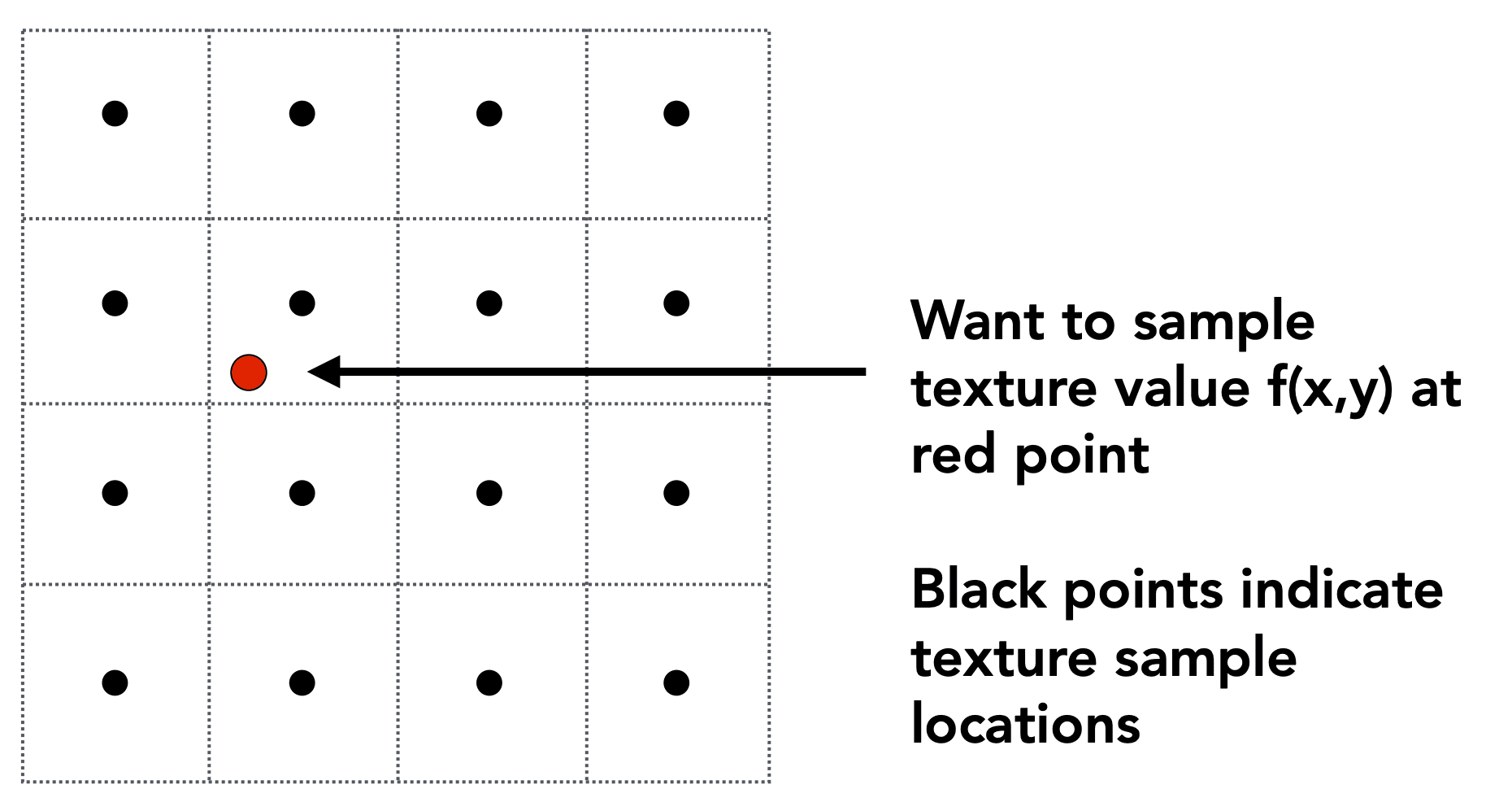
Take 4 nearest sample locations, with texture values as labeled. And fractional offsets,
Linear interpolation
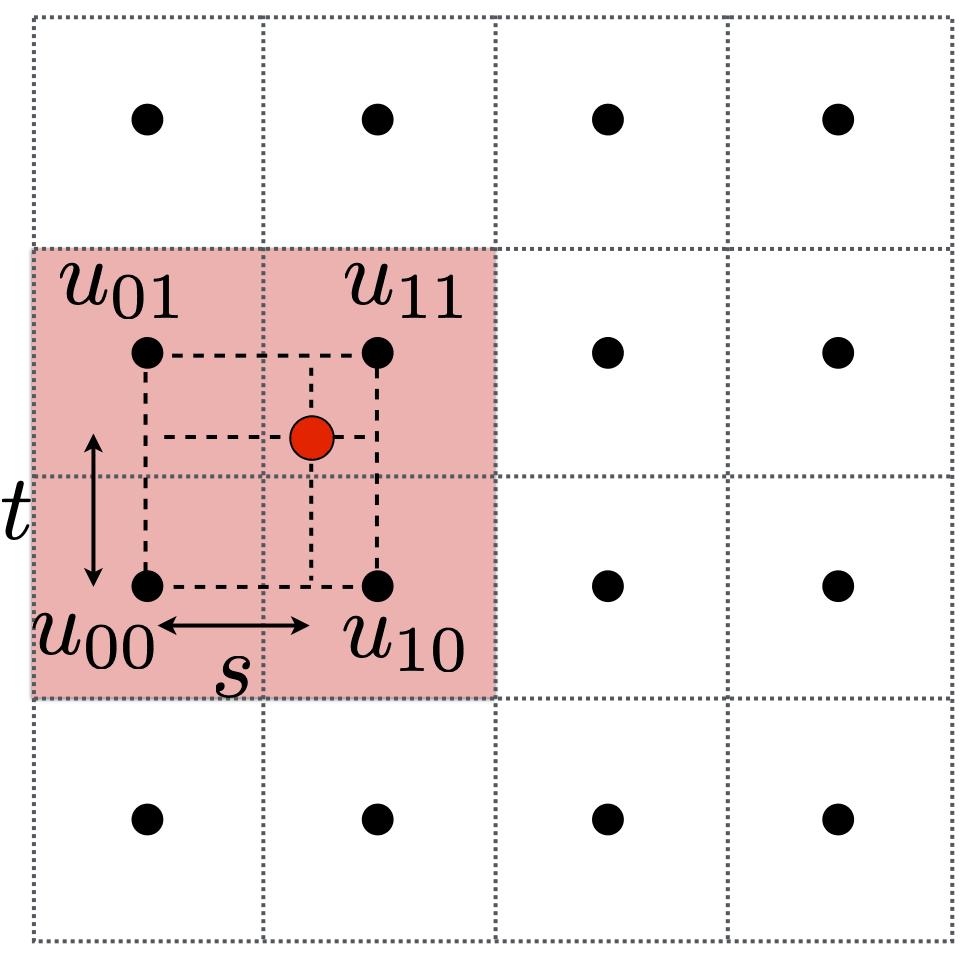
Two helper lerps (horizontal)
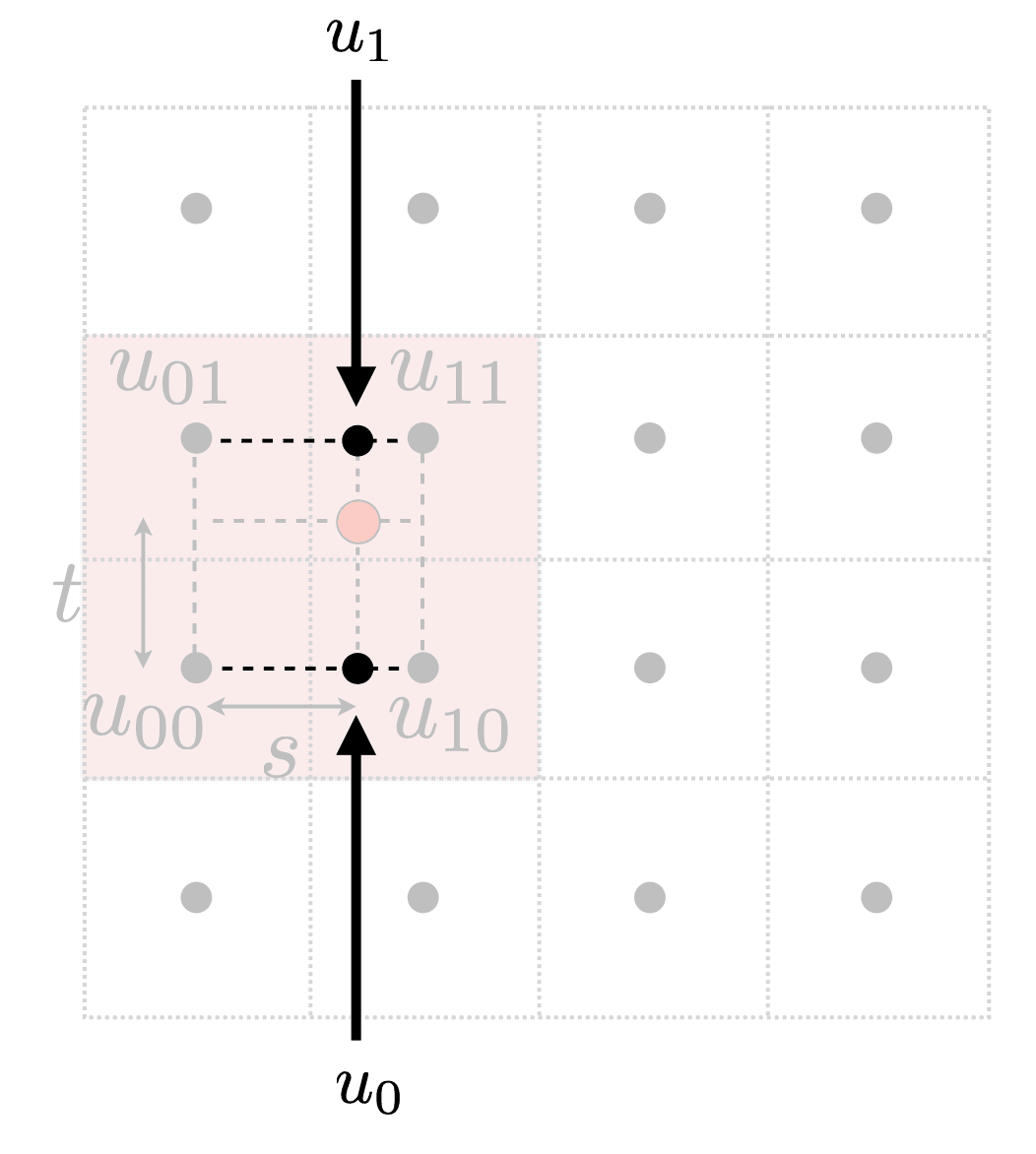
Final vertical lerp, to get result:
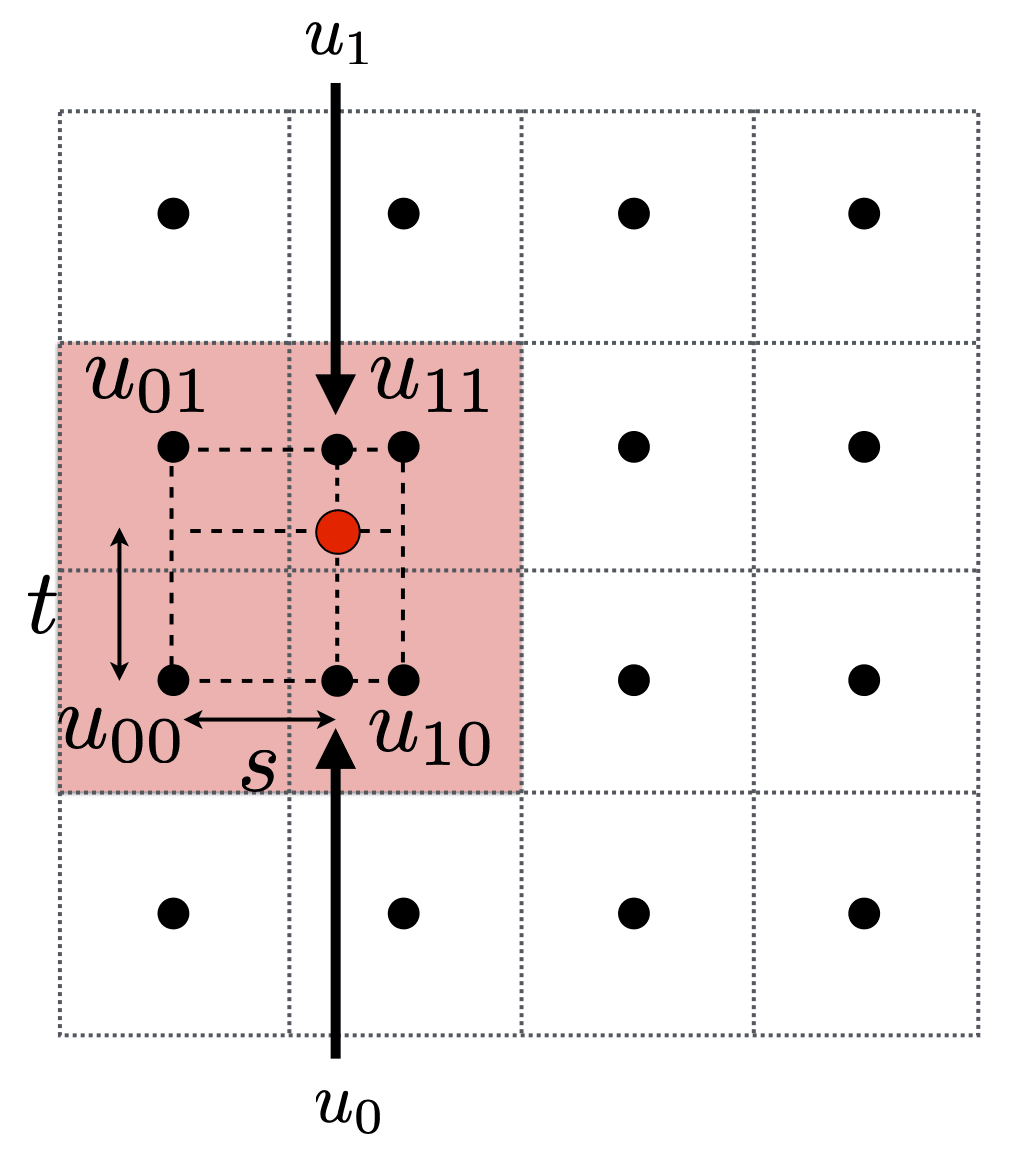
Bicubic interpolation: 取邻近 16 个 pixel 插值

What if the texture is too large?

Antialiasing — Supersampling?
Will supersampling work?
- Yes, high quality, but costly
- When highly minified, many texels in pixel footprint
- Signal frequency too large in a pixel
- Need even higher sampling frequency
Let's understand this problem in another way
- What if we don't sample?
- Just need to get the average value within a range!
Point Query vs. (Avg.) Range Query
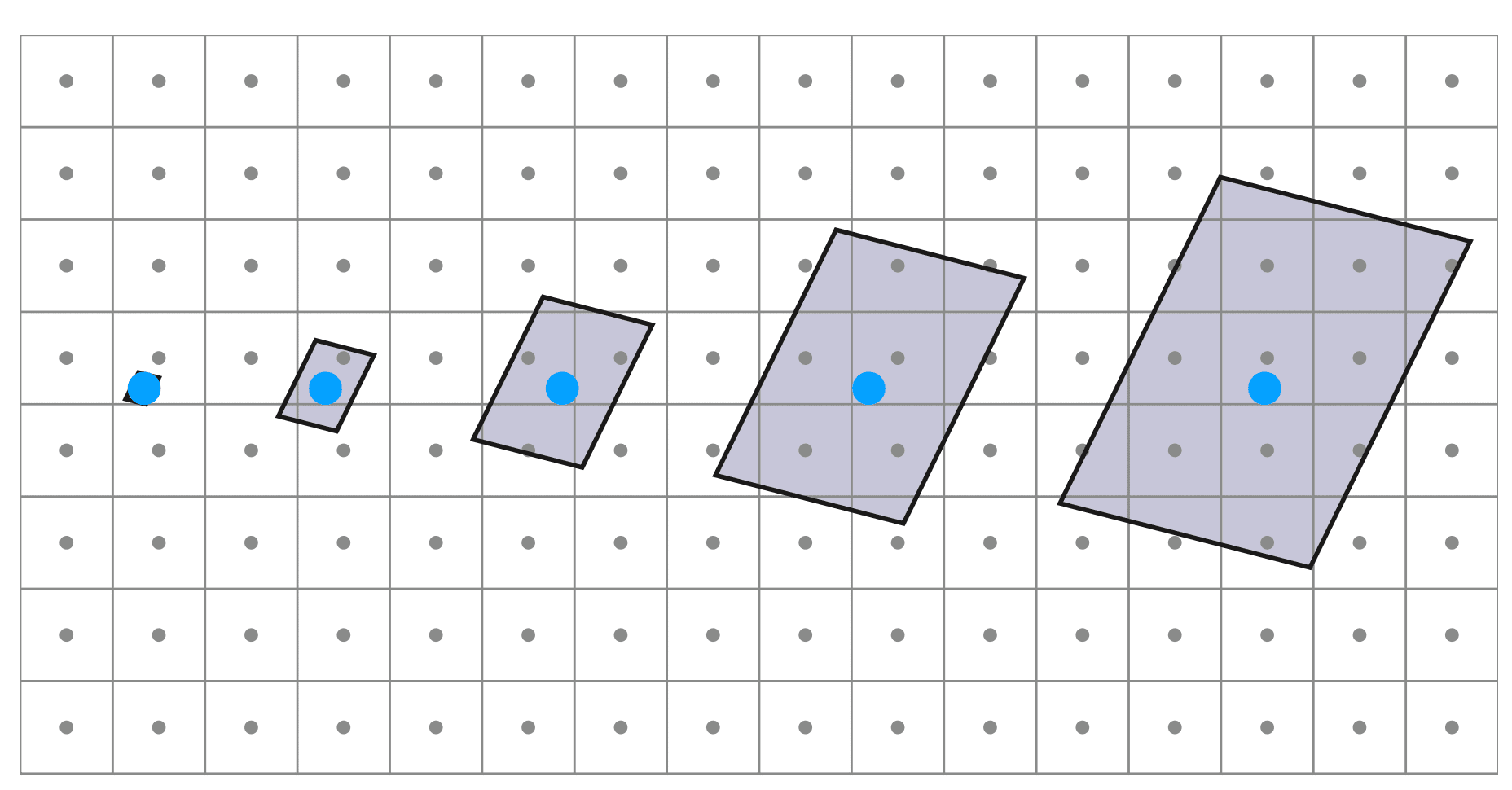
Mipmap
Allowing (fast, approx.,square) range queries

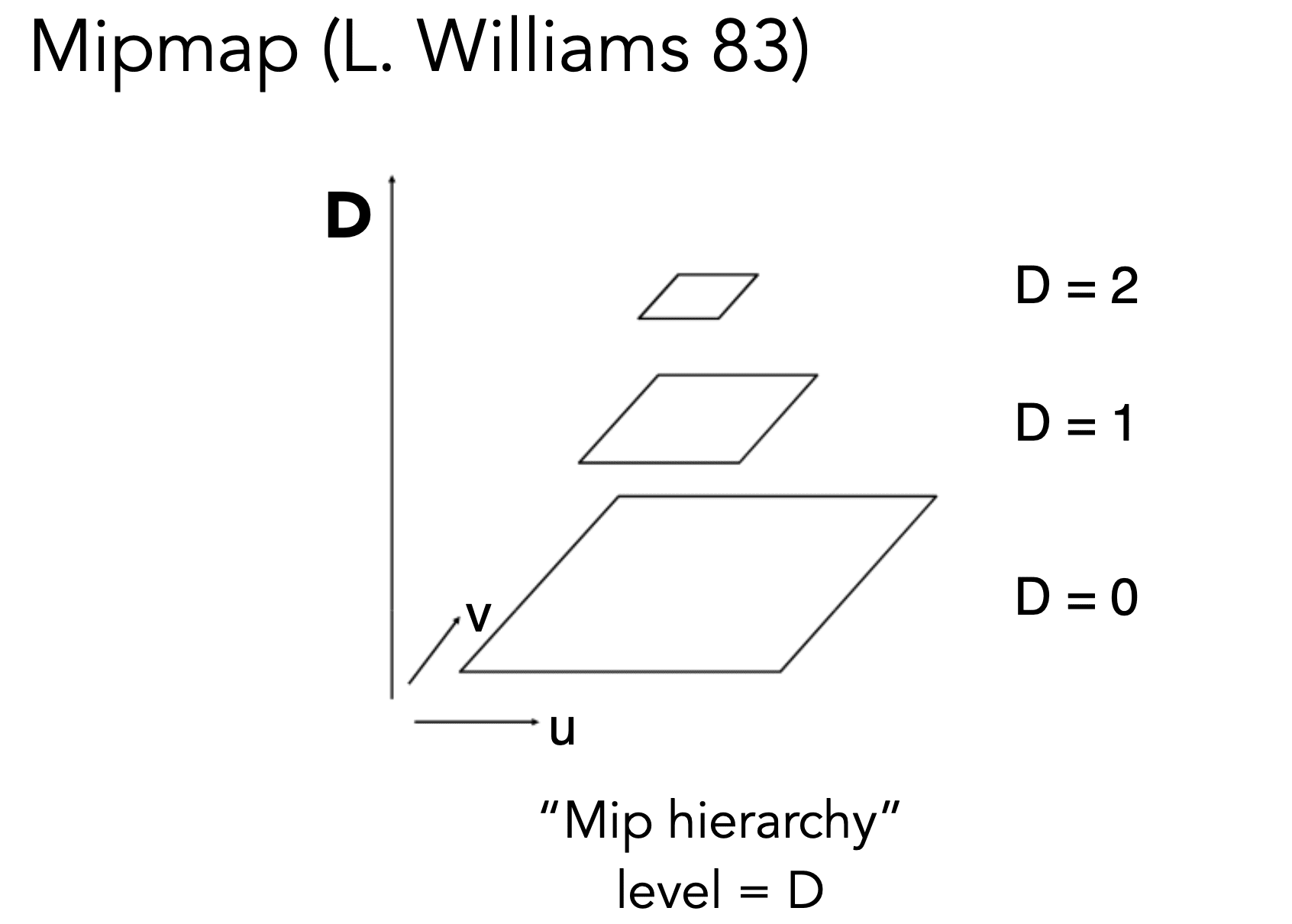
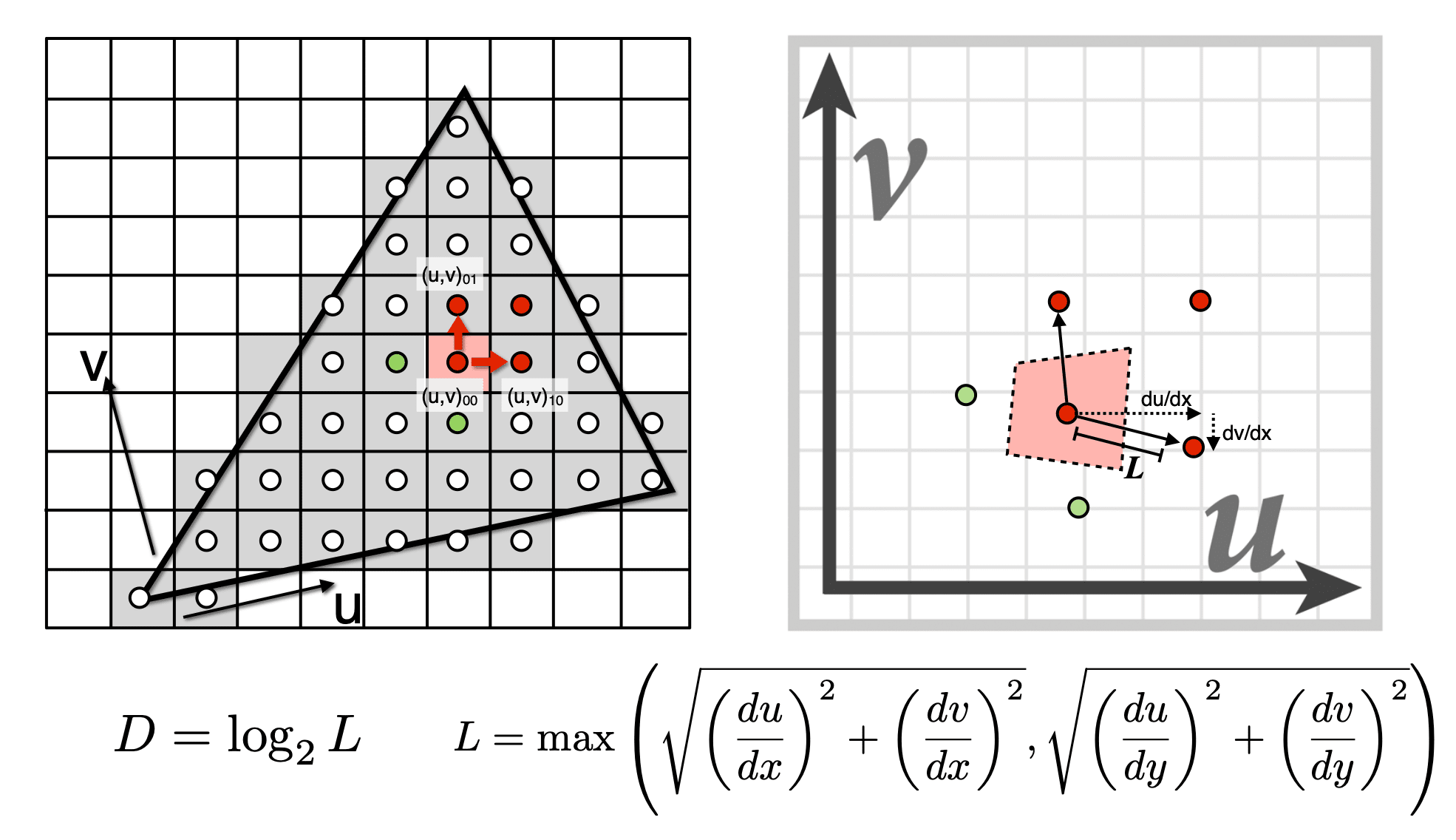
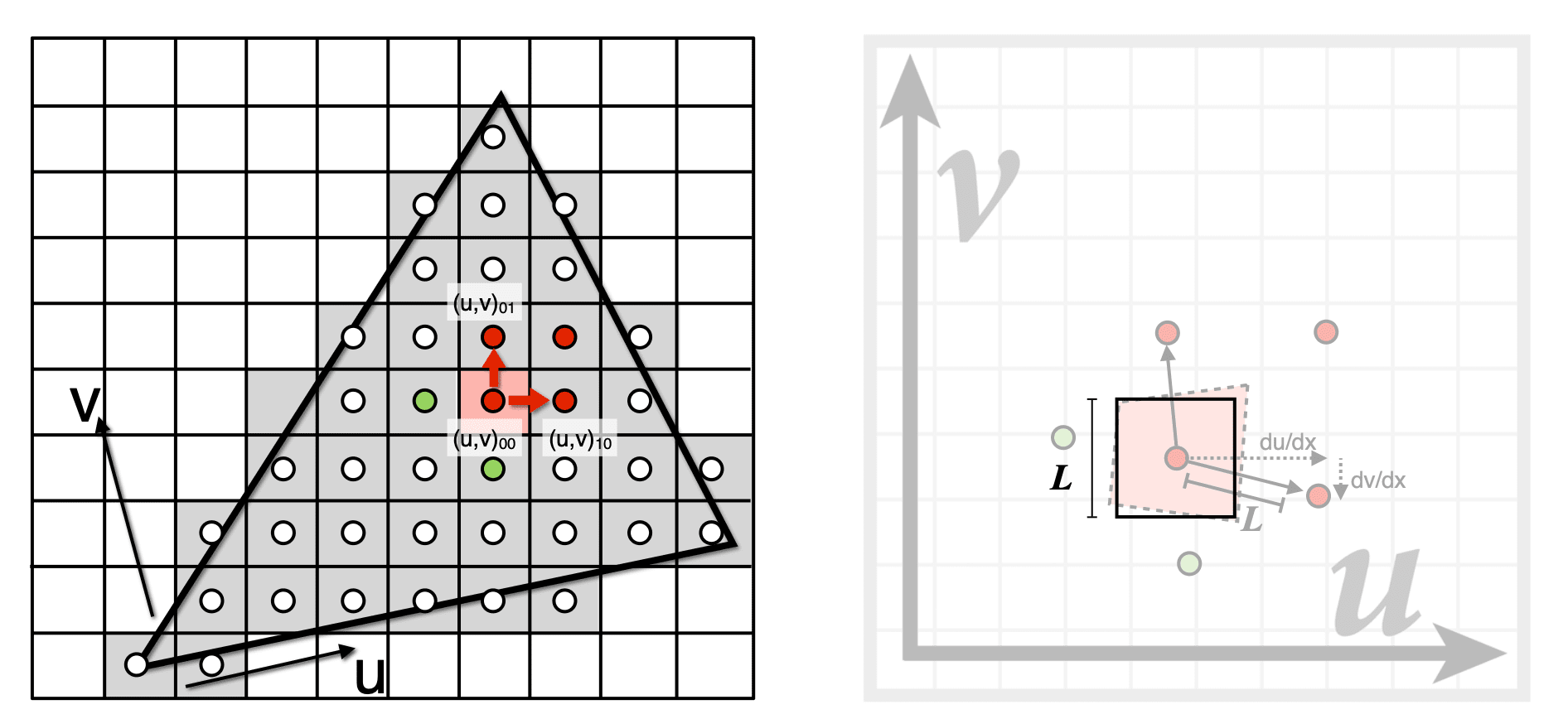
在第D层查询该值
**Example: **
 颜色越红,层数越低
颜色越红,层数越低
Trilinear Interpolation
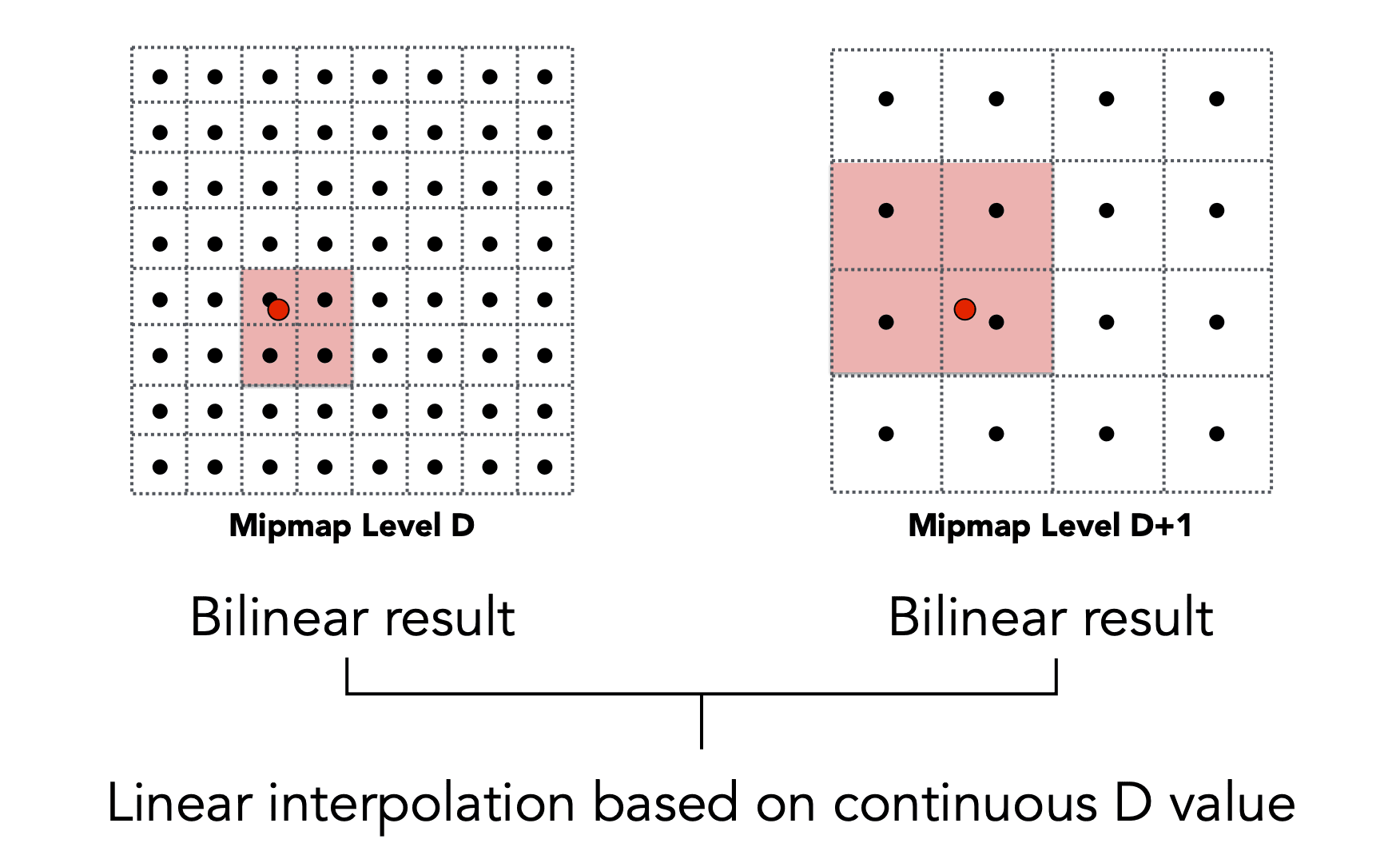

Mipmap Limitations: Overblur



Anisotropic Filtering / Ripmap
各向异性过滤
引入矩形查询,但无法解决平行四边形的查询问题

Reason: Irregular Pixel Footprint in Texture
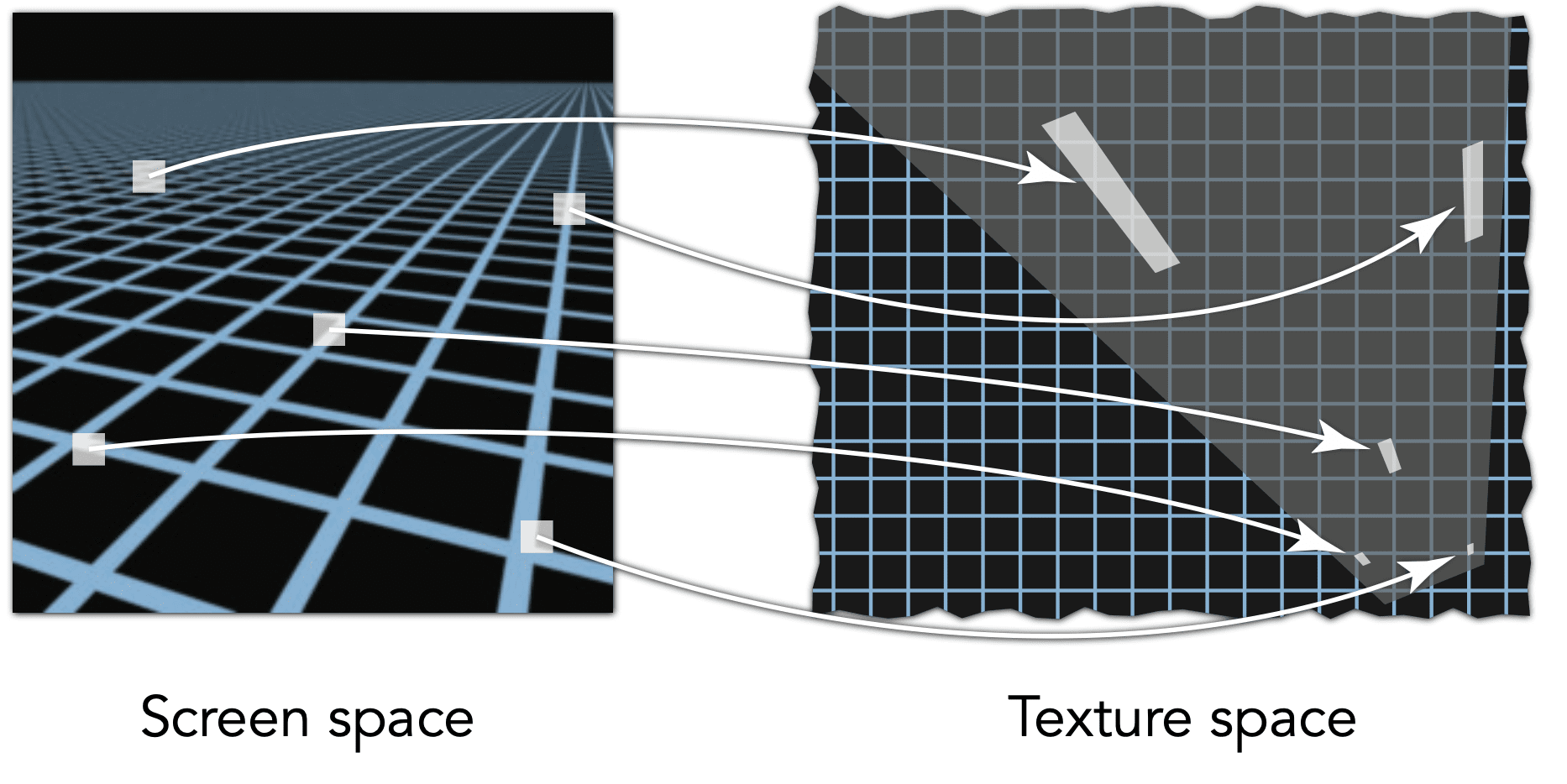

EWA filtering
- Use multiple lookups
- Weighted average
- Mipmap hierarchy still helps
- Can handle irregular footprints
Textures Application
- Environment Lighting
- Store microgeometry
- Procedural textures
- Solid modeling
- Volume rendering
- ...

